Question

13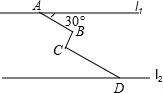．2016年清明小长假，所有高速公路对七座以下的机动车辆免收高速费，很多人都走出家门，投入大自然的环抱，进行自驾游．如图所示，在同一平面内，两条平行高速公路l₁和l₂间有一条“Z”型道路连通，其中AB段与高速公路l₁成30°角，长为20km；BC段与AB、CD段都垂直，长为10km，CD段长为30km，求两高速公路间的距离（结果保留根号）

Answer 1

分析 过B点作BE⊥l₁，交l₁于E，CD于F，l₂于G．在Rt△ABE中，根据三角函数求得BE，在Rt△BCF中，根据三角函数求得BF，在Rt△DFG中，根据三角函数求得FG，再根据EG=BE+BF+FG即可求解．

解答 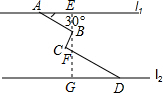解：过B点作BE⊥l₁，交l₁于E，CD于F，l₂于G．
在Rt△ABE中，BE=AB•sin30°=20×$\frac{1}{2}$=10km，
在Rt△BCF中，BF=BC÷cos30°=10÷$\frac{\sqrt{3}}{2}$=$\frac{20\sqrt{3}}{3}$km，
CF=BF•sin30°=$\frac{20\sqrt{3}}{3}$×$\frac{1}{2}$=$\frac{10\sqrt{3}}{3}$km，
DF=CD-CF=（30-$\frac{10\sqrt{3}}{3}$）km，
在Rt△DFG中，FG=DF•sin30°=（30-$\frac{10\sqrt{3}}{3}$）×$\frac{1}{2}$=（15-$\frac{5\sqrt{3}}{3}$）km，
∴EG=BE+BF+FG=（25+5$\sqrt{3}$）km．
故两高速公路间的距离为（25+5$\sqrt{3}$）km．

点评 此题考查了解直角三角形的应用，主要是三角函数的基本概念及运算，关键把实际问题转化为数学问题加以计算．