题目内容
19.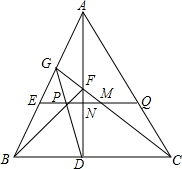 已知,如图,EQ∥BC,AD交BC于D,交EQ于N,CG交EQ于M,交AD于F,连接GD、BF交EQ于点P.求证:PM=MQ.
已知,如图,EQ∥BC,AD交BC于D,交EQ于N,CG交EQ于M,交AD于F,连接GD、BF交EQ于点P.求证:PM=MQ.
分析 根据已知条件得到△AEN∽△ABD,△AQN∽△ACD,根据相似三角形的性质得到$\frac{QN}{CD}=\frac{AN}{AD}$,$\frac{NE}{BD}=\frac{AN}{AD}$,等量代换得到$\frac{QN}{NE}=\frac{CD}{BD}$,同理$\frac{NM}{PN}=\frac{CD}{BD}$,由等式的性质得到$\frac{QN}{NE}=\frac{MN}{PN}$=$\frac{CD}{BD}$然后根据比例的性质即可得到结论.
解答 证明:∵EQ∥BC,
∴△AEN∽△ABD,△AQN∽△ACD,
∴$\frac{QN}{CD}=\frac{AN}{AD}$,$\frac{NE}{BD}=\frac{AN}{AD}$,
∴$\frac{QN}{CD}=\frac{NE}{BD}$,
∴$\frac{QN}{NE}=\frac{CD}{BD}$,
同理$\frac{NM}{PN}=\frac{CD}{BD}$,
∴$\frac{QN}{NE}=\frac{MN}{PN}$=$\frac{CD}{BD}$
同理$\frac{PM}{PE}=\frac{CD}{BD}$,
∴$\frac{NQ-NM}{EN-PN}=\frac{CD}{BD}$,
即$\frac{MQ}{PE}=\frac{CD}{BD}$,
∴$\frac{PM}{PE}=\frac{MQ}{PE}$,
∴PM=MQ.
点评 本题考查了相似三角形的判定和性质,比例的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
13.化简$\frac{5{x}^{3}y}{15{x}^{2}{y}^{2}}$的结果( )
| A. | $\frac{x}{10y}$ | B. | $\frac{{x}^{3}y}{10{x}^{2}{y}^{2}}$ | C. | $\frac{x}{3y}$ | D. | $\frac{{x}^{3}y}{3{x}^{2}{y}^{2}}$ |
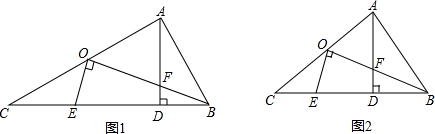
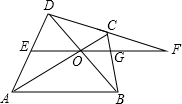 如图,四边形ABCD中,AC、BD交于O,过O作直线EF∥AB,交AD、BC于E,G,交DC延长线于F,求证:FO2=FG•FE.
如图,四边形ABCD中,AC、BD交于O,过O作直线EF∥AB,交AD、BC于E,G,交DC延长线于F,求证:FO2=FG•FE.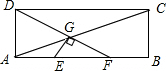 如图,矩形ABCD中,AB=3AD,E、F在AB上,且AE=EF=FB,AC交DF于G,连接EG.求证:EG⊥DF.
如图,矩形ABCD中,AB=3AD,E、F在AB上,且AE=EF=FB,AC交DF于G,连接EG.求证:EG⊥DF.