题目内容
16.某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元.为了扩大销量、增加赢利,商场决定采取适当降价的措施.经调查发现,一件衬衫每降价1元,商场平均每天可多售2件.设一件衬衫降价x元(x为整数),每天赢利y元.(1)用含x的代数式表示y,并写出x的取值范围;
(2)分别计算当x=2、20时y的值.
分析 (1)根据题意列出相应的函数关系式并确定x的取值范围.
(2)根据第一问中的函数关系式,求出x=2、20时y的值.
解答 解:(1)根据题意可得,
y=(40-x)(20+2x).
∵$\left\{\begin{array}{l}{x≥0}\\{40-x≥0}\end{array}\right.$
∴0≤x≤40.(x为整数)
故y=(40-x)(20+2x),0≤x≤40.(x为整数)
(2)令x=2,则y=(40-2)×(20+2×2)=38×(20+4)=38×24=912.
令x=20,则y=(40-20)×(20+2×20)=20×(20+40)=20×60=1200.
故x=2时,y=912;x=20时,y=1200.
点评 本题考查根据题意如何列出函数关系式,如何确定自变量的取值范围,当自变量的值一定时,可以求得相应的函数值.

练习册系列答案
相关题目
11.一元二次方程2x2+6x=9的二次项系数、一次项系数、常数项分别是( )
| A. | 2,6,9 | B. | 6,2,9 | C. | 2,6,-9 | D. | 6,2,-9 |
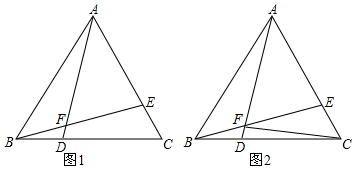
 如图所示,已知∠1=∠2,∠3=∠4.求证:AB=AC.
如图所示,已知∠1=∠2,∠3=∠4.求证:AB=AC.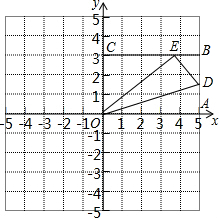 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,B(5,3)在AB边上取一点F,将纸片沿OD翻折,使点A落在BC边上的点E处,求点D,E的坐标.
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,B(5,3)在AB边上取一点F,将纸片沿OD翻折,使点A落在BC边上的点E处,求点D,E的坐标.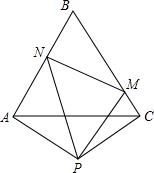 如图,等边△ABC的边长为2,且PA=PC,∠APC=120°,现有∠MPN=60°,将∠MPN绕着P点旋转,使其两边分别与AB、BC交于点N、M.试判断在旋转过程中,△BMN的周长是否发生变化?若不变,请求出周长;若变化,请说明理由.
如图,等边△ABC的边长为2,且PA=PC,∠APC=120°,现有∠MPN=60°,将∠MPN绕着P点旋转,使其两边分别与AB、BC交于点N、M.试判断在旋转过程中,△BMN的周长是否发生变化?若不变,请求出周长;若变化,请说明理由.