题目内容
17.在△ABC中,∠A=90°,∠B的平分线交AC于点D,交BC边上的高AH于点E,过D作DF⊥BC于点F.求证:四边形AEFD是菱形.分析 根据全等三角形的判定定理HL进行证明Rt△BDF≌Rt△BDA(HL),得到∠ADE=∠FDE;根据平行线的性质、角平分线的性质以及等量代换推知∠EDA=∠AED,易证AD=AE;从而根据邻边相等的平行四边形是菱形进行判断.
解答 证明:∵∠BAC=90°,
∴AC⊥EC.
又∵AD⊥AB,BD是∠ABC的平分线,
∴FD=AD.
在Rt△BDF与Rt△BDA中,
$\left\{\begin{array}{l}{FD=AD}\\{BD=BD}\end{array}\right.$,
∴Rt△BDF≌Rt△BDA(HL);
∴∠ADE=∠FDE,
∵AH是BC边上的高,
∴AH⊥BC.
又∵DF⊥BC,
∴AH∥DF,
∴∠AED=∠FDE.
∴∠EDA=∠AED,
∴AD=AE,
∴AD=DF=AE.
又∵DF∥AD,
∴四边形AEFD是菱形.
点评 本题考查了菱形的判定、全等三角形的判定与性质等知识点.菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.

练习册系列答案
相关题目
7.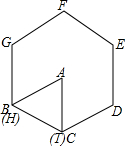 正△ABC与正六边形DEFGH的边长相等,初始如图所示,将三角形绕点I顺时针旋转使得AC与CD重合,再将三角形绕点D顺时针旋转使得AB与DE重合,…,按这样的方式将△ABC旋转2015次后,△ABC中与正六边形DEFGHI重合的边是( )
正△ABC与正六边形DEFGH的边长相等,初始如图所示,将三角形绕点I顺时针旋转使得AC与CD重合,再将三角形绕点D顺时针旋转使得AB与DE重合,…,按这样的方式将△ABC旋转2015次后,△ABC中与正六边形DEFGHI重合的边是( )
 正△ABC与正六边形DEFGH的边长相等,初始如图所示,将三角形绕点I顺时针旋转使得AC与CD重合,再将三角形绕点D顺时针旋转使得AB与DE重合,…,按这样的方式将△ABC旋转2015次后,△ABC中与正六边形DEFGHI重合的边是( )
正△ABC与正六边形DEFGH的边长相等,初始如图所示,将三角形绕点I顺时针旋转使得AC与CD重合,再将三角形绕点D顺时针旋转使得AB与DE重合,…,按这样的方式将△ABC旋转2015次后,△ABC中与正六边形DEFGHI重合的边是( )| A. | AB | B. | BC | C. | AC | D. | 无法确定 |
15.两个无理数的积一定是( )
| A. | 不是有理数 | B. | 不是无理数 | C. | 不是1 | D. | 不是0 |
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{6}{x}$的图象相交于A(2,m),B(n,1)两点,连接OA,OB,则△OAB的面积为( )
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{6}{x}$的图象相交于A(2,m),B(n,1)两点,连接OA,OB,则△OAB的面积为( )