题目内容
8．若$\frac{x-10}{{x}^{2}-4}$=$\frac{A}{x+2}$+$\frac{B}{x-2}$．求A+B的值．分析 已知等式右边通分并利用同分母分式的加法法则计算，利用分式相等的条件求出A与B的值，即可确定出A+B的值．
解答 解：$\frac{x-10}{（x+2）（x-2）}$=$\frac{A（x-2）+B（x+2）}{（x+2）（x-2）}$，
可得x-10=（A+B）x+2B-2A，即$\left\{\begin{array}{l}{A+B=1}\\{2B-2A=-10}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{A=3}\\{B=-2}\end{array}\right.$，
则A+B=3-2=0．
点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
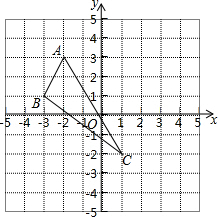已知△ABC在平面直角坐标系中的位置如图所示
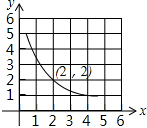已知反比例函数y=$\frac{k}{x}$的图象经过点（2，2）．