题目内容
19.已知抛物线y=3ax2+2bx+c,(1)若a=3k,b=5k,c=k+1,试说明此类函数图象都具有的性质;
(2)若a=$\frac{1}{3}$,c=2+b且抛物线在-2≤x≤2区间上的最小值是-3,求b的值;
(3)若a+b+c=1,是否存在实数x,使得相应的y的值为1,请说明理由.
分析 (1)将a=3k,b=5k,c=k+1代入y=3ax2+2bx+c,可化为y=9kx2+10kx+k+1=(9x2+10x+1)k+1,令9x2+10x+1=0,解得${x_1}=-1,{x_2}=-\frac{1}{9}$,即可求得图象必过(-1,1),($-\frac{1}{9}$,1),根据对称轴公式求得x=-$\frac{10k}{2×9k}$=$-\frac{5}{9}$.
(2)a=$\frac{1}{3}$,c=2+b,则抛物线可化为y=x2+2bx+b+2,其对称轴为x=-b,以-1≤x≤2为区间,讨论b的取值,根据最小值为-3,可得出方程,求出b的值即可.
(3)由y=1得3ax2+2bx+c=1,表示出方程的判别式的表达式,利用配方法及完全平方的非负性即可判断出结论;
解答 解:(1)∵a=3k,b=5k,c=k+1,
∴抛物线y=3ax2+2bx+c可化为y=9kx2+10kx+k+1=(9x2+10x+1)k+1
∴令9x2+10x+1=0,
解得${x_1}=-1,{x_2}=-\frac{1}{9}$
∴图象必过(-1,1),($-\frac{1}{9}$,1),
∴对称轴为直线x=-$\frac{10k}{2×9k}$=$-\frac{5}{9}$.
(2)∵a=$\frac{1}{3}$,c=2+b,
∴抛物线y=3ax2+2bx+c可化为y=x2+2bx+2+b
∴对称轴为直线x=-b
当-b>2时即b<-2,
x=2时y取到最小值为-3.
∴4+4b+2+b=-3,解得b=$-\frac{9}{5}$(不符合),
当-b<2时即b>-2,
x=2时y取到最小值为-3.
∴4+4b+2+b=-3,解得b=3;
当-2<-b<2时即-2<b<2,$\frac{{4ac-{b^2}}}{4a}=\frac{{4(2+b)-4{b^2}}}{4}=-3$
解得:${b_1}=\frac{{1+\sqrt{21}}}{2}(不符合),{b_2}=\frac{{1-\sqrt{21}}}{2}$,
∴b=3或$\frac{{1-\sqrt{21}}}{2}$,
(3)∵a+b+c=1,
∴c-1=-a-b
令y=1,则3ax2+2bx+c=1.
△=4b2-4(3a)(c-1),
∴△=4b2+4(3a)(a+b)=9a2+12ab+4b2+3a2=(3a+2b)2+3a2,
∵a≠0,
∴(3a+2b)2+3a2>0,
∴△>0,
∴存在必实数x,使得相应的y的值为1.
点评 本题考查了二次函数的综合,涉及了一元二次方程的解,求根公式及根与系数的关系,解答本题的难点在第二问,关键是分类讨论,此题难度较大.

 阅读快车系列答案
阅读快车系列答案| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |
| A. | 有一组邻边相等的四边形是菱形 | |
| B. | 对角线互相平分的平行四边形是正方形 | |
| C. | 有一个角是直角的平行四边形是矩形 | |
| D. | 一组对边相等的四边形是平行四边形 |
| A. | $\frac{34}{55}$ | B. | $\frac{21}{34}$ | C. | $\frac{55}{89}$ | D. | $\frac{89}{144}$ |
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{3y}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{3y}$ |
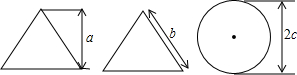
| A. | a2+c2=b2 | B. | a2+b2=4c2 | C. | a2+b2=c2 | D. | a2+4c2=b2 |

 如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )
如图,数轴的单位长度为1,如果P,Q表示的数互为相反数,那么图中的4个点中,哪一个点表示的数的平方值最大( )