题目内容
7.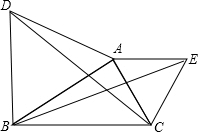 如图,△ABD,△AEC都是等边三角形,线段BE与DC有怎样的数量关系?请用旋转的性质说明上述关系成立的理由.
如图,△ABD,△AEC都是等边三角形,线段BE与DC有怎样的数量关系?请用旋转的性质说明上述关系成立的理由.
分析 利用等边三角形的性质证明△BAE≌△DAC即可.
解答 解:BE=CD,理由是:
∵△ABD,△AEC都是等边三角形,
∴AC=AE,AB=AD,∠CAE=∠DAB=60°,
∴∠BAE=∠DAC,
在△BAE和△DAC中,
∵$\left\{\begin{array}{l}{AC=AE}\\{∠BAE=∠DAC}\\{AB=AD}\end{array}\right.$,
∴△BAE≌△DAC(SAS),
∴BE=CD.
点评 本题主要考查等边三角形的性质及全等三角形的判定和性质的运用,解题的关键是能利用等边三角形的性质得到相等的线段和相等的角,从而证得三角形全等,进一步证得结论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.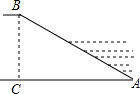 如图所示,河堤横断面迎水坡AB的坡比是1:2,坡高BC=5m,则坡面AB的长度( )
如图所示,河堤横断面迎水坡AB的坡比是1:2,坡高BC=5m,则坡面AB的长度( )
 如图所示,河堤横断面迎水坡AB的坡比是1:2,坡高BC=5m,则坡面AB的长度( )
如图所示,河堤横断面迎水坡AB的坡比是1:2,坡高BC=5m,则坡面AB的长度( )| A. | 10m | B. | 10$\sqrt{3}$m | C. | 5$\sqrt{3}$m | D. | 5$\sqrt{5}$m |
17.若x=2是方程ax+2x=16-a的解,则a的值是( )
| A. | 3 | B. | 6 | C. | 5 | D. | 4 |
 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1.
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1. 如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)的图象都经过点A(m,2),求反比例函数的解析式,并根据图象比较y1和y2的大小(x>0).
如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)的图象都经过点A(m,2),求反比例函数的解析式,并根据图象比较y1和y2的大小(x>0).