题目内容
18.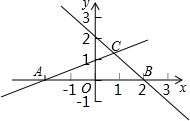 如图,l1表示直线y=-x+2,l2表示直线y=$\frac{1}{2}$x+1,l1与x轴交于B,l2交x轴于点A,l1与l2交于点C,试求A,B,C三点坐标及△ABC的面积.
如图,l1表示直线y=-x+2,l2表示直线y=$\frac{1}{2}$x+1,l1与x轴交于B,l2交x轴于点A,l1与l2交于点C,试求A,B,C三点坐标及△ABC的面积.
分析 直接利用直线l1与直线l2的解析式组成方程组即可求出点C坐标;利用两条直线的解析式可以分别求出A、B两点的坐标,结合图形即可求出△ABC的面积.
解答 解:∵l1与l2交于点C,
∴$\left\{\begin{array}{l}{y=-x+2}\\{y=\frac{1}{2}x+1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{4}{3}}\end{array}\right.$,
∴C点坐标为($\frac{2}{3}$,$\frac{4}{3}$);
令y=0分别代入直线l1、l2解析式得,
x=2,或x=-2,
∴A(2,0),B(-2,0),
∴S△ABC=$\frac{1}{2}$×4×$\frac{4}{3}$=$\frac{8}{3}$.
点评 此题主要考查了两条直线相交或平行问题,求函数与坐标轴的交点,与两个函数的交点问题,建立方程组是解决问题的关键.

练习册系列答案
相关题目
9.化简$\frac{16±4\sqrt{2}}{2}$的结果是( )
| A. | 8$±2\sqrt{2}$ | B. | 4$±2\sqrt{2}$ | C. | 4$±2\sqrt{2}$ | D. | 8$±2\sqrt{2}$ |
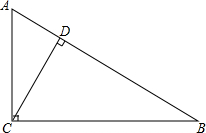 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,且AC=2,CD=$\sqrt{3}$,CB=2$\sqrt{3}$,AD=1,BD=3,试找出图中各对相似的三角形,并指出它们的相似比.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,且AC=2,CD=$\sqrt{3}$,CB=2$\sqrt{3}$,AD=1,BD=3,试找出图中各对相似的三角形,并指出它们的相似比.