题目内容
6.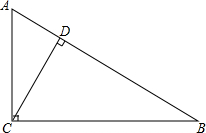 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,且AC=2,CD=$\sqrt{3}$,CB=2$\sqrt{3}$,AD=1,BD=3,试找出图中各对相似的三角形,并指出它们的相似比.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,且AC=2,CD=$\sqrt{3}$,CB=2$\sqrt{3}$,AD=1,BD=3,试找出图中各对相似的三角形,并指出它们的相似比.
分析 根据条件可以得出∠1=∠A,∠2=∠B,就可以得出△ADC∽△CDB∽△ACB,就可以得出结论相似三角形的数量为3对,由相似三角形的性质即可求出其相似比.
解答 解:∵CD⊥AB,
∴∠3=∠4=90°,
∴∠2+∠A=90°,∠1+∠B=90°.
∵∠ACB=90°,
∴∠1+∠2=90°,∠ACB=∠3=∠4.
∴∠1=∠A,∠2=∠B.
∴△ADC∽△CDB,△CDB∽△ACB,△ADC∽△ACB.
∴图中相似的三角形有3对,
∵AC=2,CD=$\sqrt{3}$,CB=2$\sqrt{3}$,AD=1,BD=3,
∴其相似比分别为2:3,$\sqrt{3}$:2,1:2$\sqrt{3}$.
点评 本题考查了垂直的性质的性质的运用,直角三角形的性质的运用,相似三角形的判定的运用,解答时找到两组对应角相等是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.$3×(-\frac{4}{7})÷(-\frac{3}{7})-(-1)^{2}$的值为( )
| A. | 3 | B. | -3 | C. | 5 | D. | -5 |
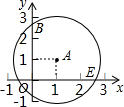 如图,在平面直角坐标系中,以A(1,1)为圆心,2为半径作⊙A,求⊙A与两坐标轴交点的坐标.
如图,在平面直角坐标系中,以A(1,1)为圆心,2为半径作⊙A,求⊙A与两坐标轴交点的坐标.
 如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上,若AB=5cm,BD=3cm,求BE的长.
如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上,若AB=5cm,BD=3cm,求BE的长.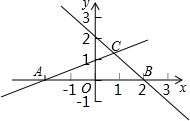 如图,l1表示直线y=-x+2,l2表示直线y=$\frac{1}{2}$x+1,l1与x轴交于B,l2交x轴于点A,l1与l2交于点C,试求A,B,C三点坐标及△ABC的面积.
如图,l1表示直线y=-x+2,l2表示直线y=$\frac{1}{2}$x+1,l1与x轴交于B,l2交x轴于点A,l1与l2交于点C,试求A,B,C三点坐标及△ABC的面积. 如图,有一个面积是120平方米的长方形养鸡场,鸡场的一边靠墙,墙长16米,与墙垂直的两侧均有一个1米宽的小门,除门外都用竹篱笆围成.若竹篱笆的总长30米,则鸡场的两邻边长各是多少?
如图,有一个面积是120平方米的长方形养鸡场,鸡场的一边靠墙,墙长16米,与墙垂直的两侧均有一个1米宽的小门,除门外都用竹篱笆围成.若竹篱笆的总长30米,则鸡场的两邻边长各是多少?