题目内容
15.若定义[a]表示不大于实数a的最大整数(例如当-2≤a<-1时,[a]=-2;0≤a<1时,[a]=0),定义{a}=a-[a].若当2≤x≤$\frac{5}{2}$时,函数y=m{x}+n的最小值为8,最大值为10,则m+n=( )| A. | 6 | B. | 10 | C. | 6或12 | D. | 6或10 |
分析 由x的取值范围结合{a}的定义即可得出0≤{x}≤$\frac{1}{2}$,根据函数y=m{x}+n的最小值为8、最大值为10结合一次函数的性质即可得出关于m、n的二元一次方程组,解之即可得出m、n的值,将其代入m+n中即可得出结论.
解答 解:∵2≤x≤$\frac{5}{2}$,
∴0≤{x}≤$\frac{1}{2}$.
∵函数y=m{x}+n的最小值为8,最大值为10,
∴$\left\{\begin{array}{l}{n=8}\\{\frac{1}{2}m+n=10}\end{array}\right.$或$\left\{\begin{array}{l}{n=10}\\{\frac{1}{2}m+n=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=4}\\{n=8}\end{array}\right.$或$\left\{\begin{array}{l}{m=-4}\\{n=10}\end{array}\right.$,
∴m+n=4+8=12或m+n=-4+10=6.
故选C.
点评 本题考查了一次函数的性质以及解二元一次方程组,根据一次函数的单调性找出关于m、n的二元一次方程组是解题的关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在边上从点B出发,沿B-C-A的线路向点A移动,每秒移动$\frac{1}{2}$cm,设移动时间为x(秒),△ABD的面积为y(cm2).
如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在边上从点B出发,沿B-C-A的线路向点A移动,每秒移动$\frac{1}{2}$cm,设移动时间为x(秒),△ABD的面积为y(cm2).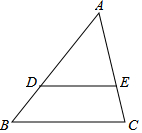 如图,画线段DE平行于BC,端点D,E分别在AB,AC上,再画线段FG平行于CA,HI平行于AB,端点也都分别在另两边上,在按上述要求画出的图形中,最少有5个三角形,最多有8个三角形.
如图,画线段DE平行于BC,端点D,E分别在AB,AC上,再画线段FG平行于CA,HI平行于AB,端点也都分别在另两边上,在按上述要求画出的图形中,最少有5个三角形,最多有8个三角形.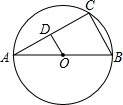 如图,AB为⊙O的直径,点C是⊙O上的一点,AB=8cm,∠A=30°,点D是弦AC上的一点,动点P从点C沿CA以2cm/s的速度向点D运动,再沿DO以1cm/s的速度向点O运动,设点P在整个运动过程中的时间为t,则t的最小值是2$\sqrt{3}$s.
如图,AB为⊙O的直径,点C是⊙O上的一点,AB=8cm,∠A=30°,点D是弦AC上的一点,动点P从点C沿CA以2cm/s的速度向点D运动,再沿DO以1cm/s的速度向点O运动,设点P在整个运动过程中的时间为t,则t的最小值是2$\sqrt{3}$s.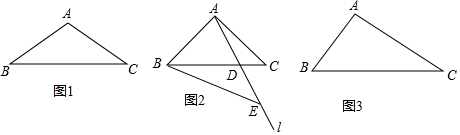
 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.点A、B 的坐标 分别是A(4,3)、B(4,1).
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.点A、B 的坐标 分别是A(4,3)、B(4,1).