��Ŀ����
7���۽�������ABC�У���BAC��90�㣬��ACB=������ABC=�£�����A��ֱ��l��BC���ڵ�D����E��ֱ��l�ϣ���BC=BE��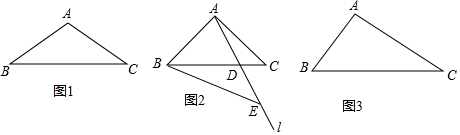
��1����AB=AC����E��AD�ӳ����ϣ�
�ٵ���=30�㣬��Dǡ��ΪBC�е�ʱ����ȫͼ1��ֱ��д����BAE=60�㣬��BEA=30�㣻
����ͼ2������BAE=2�������BEA�Ķ������ú����Ĵ���ʽ��ʾ����
��2����ͼ3����AB��AC����BEA�Ķ����루1���ТڵĽ�����ͬ��ֱ��д����BAE�������������������ϵ��
���� ��1����ֻҪ֤��AE��BC����BCE�ǵȱ������μ��ɽ�����⣮����ͼ2�У��ӳ�CA��F��ʹ��BF=BC����BF=BE=BC������BF����BM��AF��M��BN��AE��N��
ֻҪ֤��Rt��BMF��Rt��BNE���Ƴ���BEA=��F����BF=BC���Ƴ���F=��C=�����Ƴ���BEA=�����ɣ�
��2����ͼ3�У�����EC���ɡ�ADC�ס�BDE���Ƴ�$\frac{AD}{BD}$=$\frac{DC}{DE}$���Ƴ�$\frac{AD}{DC}$=$\frac{BD}{DE}$���ɡ�ADB=��CDE���Ƴ���ADB�ס�CDE���Ƴ���BAD=��DCE����ABD=��DEC=�£���BC=BE���Ƴ���BCE=��BEC���Ƴ���BAE=��BEC=��BEA+��DEC=��+�£�
��� �⣺��1���ٲ�ȫͼ1����ͼ��ʾ��
��AB=AC��BD=DC��
��AE��BC��
��EB=EC����ADB=90�㣬
�ߡ�ABC=30�㣬
���BAE=60��
��BC=BE��
���BCE�ǵȱ������Σ���DEB=��DEC��
���BEC=60�㣬��BEA=30��
�ʴ�Ϊ60��30��
����ͼ2�У��ӳ�CA��F��ʹ��BF=BC����BF=BE=BC������BF����BM��AF��M��BN��AE��N��
��AB=AC��
���ABC=��C=����
���MAB=2�����ߡ�BAN=2����
���BAM=��BAN��
��BM=BN��
��Rt��BMF��Rt��BNE��
$\left\{\begin{array}{l}{BF=BE}\\{BM=BN}\end{array}\right.$��
��Rt��BMF��Rt��BNE��
���BEA=��F��
��BF=BC��
���F=��C=����
���BEA=����
��2�����ۣ���BAE=��+�£��������£�
��ͼ3�У�����EC��
�ߡ�ACD=��BED=������ADC=��BDE��
���ADC�ס�BDE��
��$\frac{AD}{BD}$=$\frac{DC}{DE}$��
��$\frac{AD}{DC}$=$\frac{BD}{DE}$���ߡ�ADB=��CDE��
���ADB�ס�CDE��
���BAD=��DCE��
��ABD=��DEC=�£�
��BC=BE��
���BCE=��BEC��
���BAE=��BEC=��BEA+��DEC=��+�£�
���� ���⿼��ȫ�������ε��ж������ʣ����������ε��ж������ʣ����������ε����ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������λ����������ν�����⣬�����п��������ͣ�

| A�� | 2 | B�� | $\frac{1}{2}$ | C�� | -2 | D�� | -$\frac{1}{2}$ |
| A�� | 6 | B�� | 10 | C�� | 6��12 | D�� | 6��10 |
| A�� | 2x+3x=5x2 | B�� | 4a2b-5ba2=-a2b | C�� | 2a+2b=4ab | D�� | x3-x2=x |
| A�� | 3x3y��xy3 | B�� | -2016��2017 | C�� | 4ab2��-3ab2 | D�� | 2ab��1020ab |
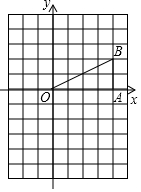 ��ͼ����ƽ��ֱ������ϵ�У���֪��B��4��2����BA��x����A��
��ͼ����ƽ��ֱ������ϵ�У���֪��B��4��2����BA��x����A��