题目内容
10.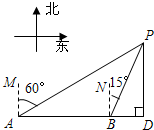 一艘轮船向正东航行,在A处测得灯塔P在A的北偏东60°方向,航行2小时到达B处,此时测得灯塔P在B的北偏东15°方向上,且灯塔P到轮船航线的距离PD是(10+10$\sqrt{3}$)海里,则轮船的航行速度为20海里/小时.
一艘轮船向正东航行,在A处测得灯塔P在A的北偏东60°方向,航行2小时到达B处,此时测得灯塔P在B的北偏东15°方向上,且灯塔P到轮船航线的距离PD是(10+10$\sqrt{3}$)海里,则轮船的航行速度为20海里/小时.
分析 过点B作BC⊥AP于点C,先求出AC=$\sqrt{3}$BC,PC=BC,再根据PD=10+10$\sqrt{3}$,求出AP,根据AP=AC+PC=$\sqrt{3}$BC+BC,求出BC,从而求出AB,最后根据路程、速度、时间之间的关系得出轮船的航行速度.
解答 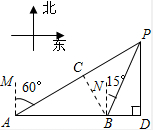 解:过点B作BC⊥AP于点C,在Rt△ABC,∠ACB=90°,∠BAC=30°,
解:过点B作BC⊥AP于点C,在Rt△ABC,∠ACB=90°,∠BAC=30°,
∵∠MAP=60°,
∴∠BAC=30°,
∴AB=2BC,AP=2PD=20+20$\sqrt{3}$,
tan30°=$\frac{BC}{AC}$,
∴AC=$\sqrt{3}$BC,
∴∠ABP=105°,
∴∠APB=45°,
∴PC=BC,
∴AP=AC+PC=$\sqrt{3}$BC+BC=20+20$\sqrt{3}$,
∴BC=20,
∴AB=40,
∵航行2小时到达B处,
∴轮船的航行速度为:40÷2=20(海里/小时).
故答案为:20.
点评 本题考查解直角三角形的应用,有一定的难度,注意在解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
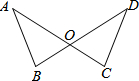 已知:如图AC=BD,AB=DC.证明:
已知:如图AC=BD,AB=DC.证明: