��Ŀ����
7��ij�о����������ˮ�����ɡ����й�ˮ�ѡ��͡���ˮ�����ѡ���������ɣ�Ϊ�˹��������Լ��ˮ�����г��й�ˮ�Ѱ�����ʽ�Ʒѣ�һ������ˮ10�����ڣ�����10�֣����û���ÿ����1.5Ԫ��һ������ˮ����10�ֵ��û���10��ˮ��ÿ��1.5Ԫ�շѣ�����10�ֵIJ��֣���ÿ��2Ԫ�շѣ�������ˮ������һ�ɰ�ÿ��0.65Ԫ��ȡ����1��ij����5�·���ˮ8�֣�Ӧ��ˮ�Ѷ���Ԫ��6�·���ˮ16�֣�Ӧ��ˮ�Ѷ���Ԫ��
��2����ij��ij����ˮx�֣������ú���x�Ĵ���ʽ��ʾӦ����ˮ�ѣ�
���� ��1������һ������ˮ10�����ڣ�����10�֣����û���ÿ����1.5Ԫ��һ������ˮ����10�ֵ��û���10��ˮ��ÿ��1.5Ԫ�շѣ�����10�ֵIJ��֣���ÿ��2Ԫ�շѺ���ˮ������ÿ��0.65Ԫ����ʽ���㼴�ɣ�
��2��������������ۣ���0��x��10ʱ��x��10ʱ���ֱ������֪������ʽ�������ɣ�
��� �⣺��1����ˮ8��ʱ��Ӧ��ˮ���ǣ�1.5��8+0.65��8=17.2��Ԫ����
��ˮ16��ʱ��Ӧ��ˮ���ǣ�1.5��10+6��2+0.65��16=37.4��Ԫ����
��2���� 0��x��10ʱ��Ӧ����ˮ���ǣ�1.5x+0.65x=2.15xԪ��
��x��10ʱ��Ӧ����ˮ���ǣ�15+2��x-10��+0.65x=��2.65x-5��Ԫ��
���� ���⿼�����д���ʽ���������Ĺؼ��Ƕ������⣬�ҵ���������ĵ�����ϵ����ϵΪ��Ӧ��ˮ��=����ˮ��+��ˮ�����ѣ�

��ϰ��ϵ�д�
�����Ŀ
17��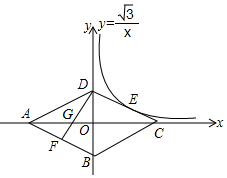 ��֪��ͼ������ABCD���ĸ���������������ϣ��Խ���AC��BD����ԭ��O��DF��AB��AC�ڵ�G������������y=$\frac{\sqrt{3}}{x}$��x��0�������߶�DC���е�E����BD=4����AG�ij�Ϊ��������
��֪��ͼ������ABCD���ĸ���������������ϣ��Խ���AC��BD����ԭ��O��DF��AB��AC�ڵ�G������������y=$\frac{\sqrt{3}}{x}$��x��0�������߶�DC���е�E����BD=4����AG�ij�Ϊ��������
 ��֪��ͼ������ABCD���ĸ���������������ϣ��Խ���AC��BD����ԭ��O��DF��AB��AC�ڵ�G������������y=$\frac{\sqrt{3}}{x}$��x��0�������߶�DC���е�E����BD=4����AG�ij�Ϊ��������
��֪��ͼ������ABCD���ĸ���������������ϣ��Խ���AC��BD����ԭ��O��DF��AB��AC�ڵ�G������������y=$\frac{\sqrt{3}}{x}$��x��0�������߶�DC���е�E����BD=4����AG�ij�Ϊ��������| A�� | $\frac{4\sqrt{3}}{3}$ | B�� | $\sqrt{3}$+2 | C�� | 2$\sqrt{3}$+1 | D�� | $\frac{3\sqrt{3}}{2}$+1 |
2����������$\sqrt{2}$��$\sqrt{16}$���С�$2.\stackrel{•}9$��0.010010001����ÿ����1֮�����ζ��0�������������ǣ�������
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
12�� ��ͼ��һ��ľ��AB�ij�Ϊ2mб��������洹ֱ��ǽ�ϣ���������б�ǡ�ABOΪ60�㣬��ľ����ǽ�����»�����A�䣬AA��=$\sqrt{3}-\sqrt{2}$��B���ص������һ�������B�䣬��ľ���е��P��֮�˶���P����������·����Ϊ��������
��ͼ��һ��ľ��AB�ij�Ϊ2mб��������洹ֱ��ǽ�ϣ���������б�ǡ�ABOΪ60�㣬��ľ����ǽ�����»�����A�䣬AA��=$\sqrt{3}-\sqrt{2}$��B���ص������һ�������B�䣬��ľ���е��P��֮�˶���P����������·����Ϊ��������
 ��ͼ��һ��ľ��AB�ij�Ϊ2mб��������洹ֱ��ǽ�ϣ���������б�ǡ�ABOΪ60�㣬��ľ����ǽ�����»�����A�䣬AA��=$\sqrt{3}-\sqrt{2}$��B���ص������һ�������B�䣬��ľ���е��P��֮�˶���P����������·����Ϊ��������
��ͼ��һ��ľ��AB�ij�Ϊ2mб��������洹ֱ��ǽ�ϣ���������б�ǡ�ABOΪ60�㣬��ľ����ǽ�����»�����A�䣬AA��=$\sqrt{3}-\sqrt{2}$��B���ص������һ�������B�䣬��ľ���е��P��֮�˶���P����������·����Ϊ��������| A�� | 1 | B�� | $\sqrt{3}$ | C�� | $\frac{��}{6}$ | D�� | $\frac{��}{12}$ |
16��ijУ�����꼶��������������Զ�IJ��ԣ���1.7mΪ��꣬����1.7m����������ʾ������1.7m���ø�����ʾ����һ��10�������ɼ����£���λ��cm����
����һ�������Ĵ���ʣ�
| +2 | -3 | 0 | +4 | +6 | -6 | 0 | +3 | 4 | 3 |




