题目内容
11.在平面直角坐标系xOy中,直线y=-$\frac{1}{2}$x+6与x轴、y轴分别交于点A、B,与直线y=x相交于点C.
(1)直接写出点C的坐标;
(2)如图,现将直角∠FCE绕直角顶点C旋转,旋转时始终保持直角边CF与x轴、y轴分别交于点F、点D,直角边CE与x轴交于点E.
①在直角∠FCE旋转过程中,$\frac{CD}{CE}$的值是否会发生变化?若改变,请说明理由;若不变,请求出这个值;
②在直角∠FCE旋转过程中,是否存在以C、E、F为顶点的三角形与△ODE相似?若存在,求出点D的坐标;若不存在,请说明理由.
分析 (1)联立两直线解析式,求方程组的解即可求得点C的坐标;
(2)①过点C作CH⊥y轴于点H,过点C作CK⊥x轴于点K,则可证明△CHD∽△CKE,结合点C的坐标,可求得$\frac{CD}{CE}$的值;
②分△ODE∽△CEF和△ODE∽△CFE两种情况,当△ODE∽△CEF时,利用相似三角形的性质可求得O为EF中点,可求得OF的长,再证明△CHD∽△FOD,利用相似三角形的性质可求得OD的长,可求得D点的坐标;当△ODE∽△CFE时,过点C作CM⊥y轴于点M,过点C作CN⊥x轴于点N,利用△CMD≌△CNE可证得OC=OD,则可求得点D的坐标.
解答 解:
(1)联立两直线解析式可得$\left\{\begin{array}{l}{y=-\frac{1}{2}x+6}\\{y=x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,
∴C(4,4);
(2)①不变;
如图1,过点C作CH⊥y轴于点H,过点C作CK⊥x轴于点K,则CH=CK=4,
∵∠1+∠DCK=90°,∠2+∠DCK=90°,
∴∠1=∠2,且∠CHD=∠CKE,
∴△CHD∽△CKE,
∴$\frac{CD}{CE}$=$\frac{CH}{CK}$=$\frac{4}{4}$=1;
②存在,
1°若△ODE∽△CEF,如图2,
则∠OED=∠CFE,
∴DF=DE,又OD⊥EF,
∴OF=OE,
∵∠FCE=90°,
∴OC=$\frac{1}{2}$EF,
在Rt△CHO中,由勾股定理得OC=$4\sqrt{2}$,
∴OE=OF=OC=4$\sqrt{2}$,
又CH∥OF,
∴△CHD∽△FOD,
∴$\frac{HD}{OD}$=$\frac{CH}{OF}$,即$\frac{4-OD}{OD}$=$\frac{4}{2\sqrt{2}}$,
∴OD=8-4$\sqrt{2}$,
∴D(0,8-4$\sqrt{2}$);
2°若△ODE∽△CFE,如图3,
则∠CEO=∠OED.
过点C作CM⊥y轴于点M,过点C作CN⊥x轴于点N,
则CM=CN=4.易证△CMD≌△CNE,
∴∠CEO=∠CDM,CD=CE,
∴△CDE为等腰直角三角形,
∴∠CED=45°,
∴∠CEO=∠OED=∠CDM=22.5°,
∵△CMO为等腰直角三角形,
∴∠COM=45°,
∴∠OCD=∠COM-∠CDM=22.5°,
∴∠OCD=∠ODC,
∴OD=OC,
在Rt△CMO中,由勾股定理得OC=4$\sqrt{2}$,
∴OD=OC=4$\sqrt{2}$,
∴D(0,-4$\sqrt{2}$);
综上所述若以C、E、F为顶点的三角形与△ODE相似,则D点坐标为(0,8-4$\sqrt{2}$)或(0,-4$\sqrt{2}$).
点评 本题为相似三角形的综合应用,涉及知识点有函数图象的交点、相似三角形的判定和性质、等腰直角三角形的性质及分类讨论思想等.在(1)中联立函数解析式构成方程组是求函数图象交点的常用方法,在(2)中利用相似三角形的性质得到关于OD的方程求得OD的长是解题的关键.本题考查知识点较多,综合性较强,难度较大.

 高效智能课时作业系列答案
高效智能课时作业系列答案| A. | -2016 | B. | -$\frac{1}{2016}$ | C. | 2016 | D. | $\frac{1}{2016}$ |
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(2)产量最多的一天比产量最少的一天多生产多少辆?
(3)赶进度期间该厂实行计件工资加浮动工资制度,即:每生产一辆车的工资为60元,超过计划完成任务每辆车则在原来60元工资上在奖励15元;比计划每少生产一辆则在应得的总工资上扣发15元(工资按日统计,每周汇总一次),求该厂工人这一周的工资总额是多少?
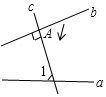 如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )| A. | 20° | B. | 30° | C. | 50° | D. | 70° |
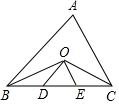 如图,等边△ABC的边长为6cm,BO,CO分别是∠ABC和∠ACB的平分线,且OD∥AB,OE∥AC.求△ODE的周长.
如图,等边△ABC的边长为6cm,BO,CO分别是∠ABC和∠ACB的平分线,且OD∥AB,OE∥AC.求△ODE的周长.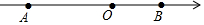 如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.
如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.