题目内容
已知a,b,c为三角形三边,比较a2+b2-c2和4a2b2的大小.
考点:因式分解的应用,三角形三边关系
专题:
分析:根据平方差公式,可分解因式得[(a+b+c)(a+b-c)][(a-b+c)(a-b-c)],根据三角形两边之和大于第三边,可得[(a+b+c)(a+b-c)][(a-b+c)(a-b-c)]<0,根据不等式的性质,可得答案.
解答:解:(a2+b2-c2)-(2ab)2=(a2+b2-c2+2ab)(a2+b2-c2-2ab)
=[(a+b)2-c2][(a-b)2-c2]
=[(a+b+c)(a+b-c)][(a-b+c)(a-b-c)],
由三角形两边之和大于第三边,得
a+b+c>,a+b-c>0,a-b+c>0,a-b-c<0.
原式=[(a+b+c)(a+b-c)][(a-b+c)(a-b-c)]<0,
即(a2+b2-c2)2<4a2b2.
开方,得
a2+b2-c2<2ab.
4a2b2-2ab=2ab(2ab-1)>0,
4a2b2>2ab>a2+b2-c2.
∴a2+b2-c2<4a2b2.
=[(a+b)2-c2][(a-b)2-c2]
=[(a+b+c)(a+b-c)][(a-b+c)(a-b-c)],
由三角形两边之和大于第三边,得
a+b+c>,a+b-c>0,a-b+c>0,a-b-c<0.
原式=[(a+b+c)(a+b-c)][(a-b+c)(a-b-c)]<0,
即(a2+b2-c2)2<4a2b2.
开方,得
a2+b2-c2<2ab.
4a2b2-2ab=2ab(2ab-1)>0,
4a2b2>2ab>a2+b2-c2.
∴a2+b2-c2<4a2b2.
点评:本题考查了因式分解的应用,利用了平方差公式,完全平方公式,不等式的性质,因式分解是解题关键.

练习册系列答案
相关题目
 在四边形ABCD中,AD∥BC,BD是∠ABC的平分线,且CD⊥BD,AD=4,CD=2.
在四边形ABCD中,AD∥BC,BD是∠ABC的平分线,且CD⊥BD,AD=4,CD=2. 在Rt△ABC中,DE垂直平分斜边AB于点D,且点E为AB的下方,DE=
在Rt△ABC中,DE垂直平分斜边AB于点D,且点E为AB的下方,DE=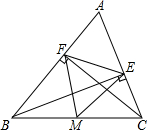 如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点.
如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点.

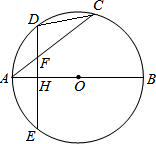 如图,已知AB、AC分别为⊙O的直径和弦,D为
如图,已知AB、AC分别为⊙O的直径和弦,D为