题目内容
12.在?ABCD中,M是AD边上一点,且AM=$\frac{1}{3}$AD,连接BD、MC相交于O点,则S△MOD:S△COB=4:9.分析 根据平行四边形的性质得出AD=BC,AD∥BC,求出$\frac{DM}{BC}$=$\frac{2}{3}$,根据相似三角形的判定得出△MOD∽△COB,根据相似得出比例式,即可得出答案.
解答 解:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AM=$\frac{1}{3}$AD,
∴$\frac{DM}{BC}$=$\frac{2}{3}$,
∵AD∥BC,
∴△MOD∽△COB,
∴$\frac{{S}_{△MOD}}{{S}_{△COB}}$=($\frac{DM}{BC}$)2=($\frac{2}{3}$)2=$\frac{4}{9}$,
故答案为:4:9.
点评 本题考查了相似三角形的性质和判定,平行四边形的性质的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
3.用四舍五入法得到的近似数2.18×104,下列说法正确的是( )
| A. | 它精确到百分位 | B. | 它精确到百位 | C. | 它精确到万位 | D. | 它精确到0.01 |
20.已知函数y=(k-1)x2-4x+4与x轴只有一个交点,则k的取值范围是( )
| A. | k≤2且k≠1 | B. | k<2且k≠1 | C. | k=2 | D. | k=2或1 |
17.|-2016|等于( )
| A. | -2016 | B. | 2016 | C. | ±2016 | D. | -$\frac{1}{2016}$ |
1.已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x1,0),且1<x1<2,与y轴交于的正半轴的交点在(0,2)的下方,下列结论:
①a<b<0;②2a+c>0;③4a-2b+c>0;④2a-b+1>0,其中正确结论个数是( )
①a<b<0;②2a+c>0;③4a-2b+c>0;④2a-b+1>0,其中正确结论个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.sin230°的相反数是( )
| A. | $-\frac{1}{4}$ | B. | $-\frac{1}{2}$ | C. | -4 | D. | -2 |
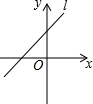 直线l:y=(2-k)x+2(k为常数),如图所示,则k的取值范围在数轴上表示为( )
直线l:y=(2-k)x+2(k为常数),如图所示,则k的取值范围在数轴上表示为( )


 如图,在菱形ABCD中,E是BC边上的点,AE交BD于点F,若EC=2BE,则$\frac{BF}{FD}$的值是$\frac{1}{3}$.
如图,在菱形ABCD中,E是BC边上的点,AE交BD于点F,若EC=2BE,则$\frac{BF}{FD}$的值是$\frac{1}{3}$.