题目内容
15.定理证明:平行四边形的对边相等.分析 根据要求,画出一个平行四边形,写出已知求证,最后利用三角形全等证明即可.
解答 已知:如图,
四边形ABCD为平行四边形.
求证:AB=CD,BC=AD.
证明:∵ABCD为平行四边形,(已知)
∴AB∥CD,AD∥BC,(平行四边形对应边相等)
∴∠DAC=∠BCA、∠BAC=∠DCA,(两直线平行,内错角相等)
∵AC=CA,(公共边)
∴△ADC≌△CBA,(AAS)
∴AB=CD,BC=AD.(全等三角形的对应边相等)
点评 本题考查了平行四边形的性质,属于证明命题的题目,此类题目解题的步骤是,先画出图形,再根据图形和原命题写出已知、求证和证明.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
10.计算3-1的结果是( )
| A. | -1 | B. | -3 | C. | 3 | D. | $\frac{1}{3}$ |
10. 如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )
如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )
 如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )
如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )| A. | 35° | B. | 55° | C. | 60° | D. | 70° |
 阅读材料:
阅读材料: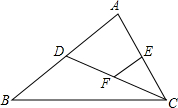 如图,CD是△ABC的中线,点E,F分别是AC、DC的中点,EF=2,则BD=4.
如图,CD是△ABC的中线,点E,F分别是AC、DC的中点,EF=2,则BD=4.