题目内容
11.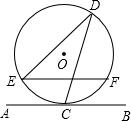 如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )
如图,如果直线AB与半径为2的⊙O相切于点C,D是⊙O上一点,且∠EDC=30°,弦EF∥AB,则EF的长是( )| A. | 2$\sqrt{3}$ | B. | 8 | C. | 2$\sqrt{10}$ | D. | 2$\sqrt{13}$ |
分析 连接OC与OE.根据一条弧所对的圆周角等于它所对的圆心角的一半,可知∠EOC的度数;再根据切线的性质定理,圆的切线垂直于经过切点的半径,可知OC⊥AB;又EF∥AB,可知OC⊥EF,最后由勾股定理可将EF的长求出
解答 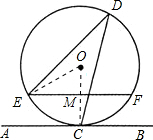 解:连接OE和OC,且OC与EF的交点为M.
解:连接OE和OC,且OC与EF的交点为M.
∵∠EDC=30°,
∴∠COE=60°.
∵AB与⊙O相切,
∴OC⊥AB,
又∵EF∥AB,
∴OC⊥EF,即△EOM为直角三角形.
在Rt△EOM中,EM=sin60°×OE=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$,
∵EF=2EM,
∴EF=2$\sqrt{3}$.
故选A.
点评 本题主要考查切线的性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.计算-2+1的结果是( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
3. 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于F,则$\frac{DF}{AD}$=( )
如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于F,则$\frac{DF}{AD}$=( )
 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于F,则$\frac{DF}{AD}$=( )
如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于F,则$\frac{DF}{AD}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |

 对于一个三角形,设其三个内角的度数分别为x°、y°和z°,若x、y、z满足x2+y2=z2,我们定义这个三角形为美好三角形.
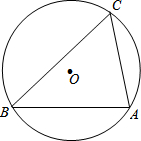
对于一个三角形,设其三个内角的度数分别为x°、y°和z°,若x、y、z满足x2+y2=z2,我们定义这个三角形为美好三角形. 如图,圆A的半径为3,P是CB延长线上一点,PO=6,PA切圆O于点A,那么圆O的切线PA的长为3$\sqrt{3}$.
如图,圆A的半径为3,P是CB延长线上一点,PO=6,PA切圆O于点A,那么圆O的切线PA的长为3$\sqrt{3}$.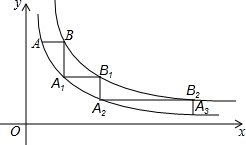 如图,在平面直角坐标系的第一象限中,y1=$\frac{4}{x}$和y2=$\frac{8}{x}$,点A(1,a)在y1=$\frac{4}{x}$上,AB∥x轴交y2=$\frac{8}{x}$于点B,BA1∥y轴交y1=$\frac{4}{x}$于点A1,A1B1∥x轴交y2=$\frac{8}{x}$于点B2,…,按照此规律作图,则B2的点坐标为(8,1).
如图,在平面直角坐标系的第一象限中,y1=$\frac{4}{x}$和y2=$\frac{8}{x}$,点A(1,a)在y1=$\frac{4}{x}$上,AB∥x轴交y2=$\frac{8}{x}$于点B,BA1∥y轴交y1=$\frac{4}{x}$于点A1,A1B1∥x轴交y2=$\frac{8}{x}$于点B2,…,按照此规律作图,则B2的点坐标为(8,1).