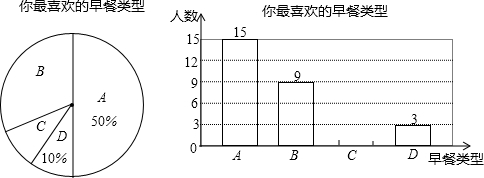
题目内容
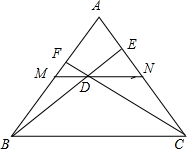 如图,在等边△ABC中,M、N分别是AB、AC的中点,D为MN上任意一点,BD、CD的延长线分别交AC、AB于点E、F,求证:
如图,在等边△ABC中,M、N分别是AB、AC的中点,D为MN上任意一点,BD、CD的延长线分别交AC、AB于点E、F,求证:| 1 |
| CE |
| 1 |
| BF |
| 3 |
| AB |
考点:相似三角形的判定与性质,等边三角形的性质
专题:证明题
分析:作辅助线构造出两对相似三角形,分别求出
、
与等边△ABC的边长之间的关系,经化简运算问题即可解决.
| 1 |
| CE |
| 1 |
| BF |
解答:解:过点D分别作DG∥BM,DK∥NC,交BC与点G、K;
则∠DGK=∠ABC,∠DKG=∠ACB;
∵△ABC是等边三角形,
∴AB=AC=BC(设为a),∠ABC=∠ACB=60°,
故∠DKG=∠DKG=60°,△DGK是等边三角形;
∴DG=GK=DK;
∵DM∥BG,DG∥BM,
∴四边形DMBG是平行四边形,DG=BM;而点M为AB的中点,
∴GK=DK=DG=BM=
a.
∵DK∥NC,
∴
=
,
=
;
同理可求:
=
,故
+
=
+
∵DG=DK=
a,BC=a,
∴
+
=
;
又∵BK+CG=(BK+CK)+GK=a+
a=
a,
∴
+
=
=
,
即
+
=
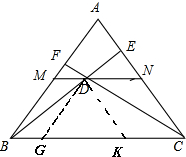
则∠DGK=∠ABC,∠DKG=∠ACB;
∵△ABC是等边三角形,
∴AB=AC=BC(设为a),∠ABC=∠ACB=60°,
故∠DKG=∠DKG=60°,△DGK是等边三角形;
∴DG=GK=DK;
∵DM∥BG,DG∥BM,
∴四边形DMBG是平行四边形,DG=BM;而点M为AB的中点,
∴GK=DK=DG=BM=
| 1 |
| 2 |
∵DK∥NC,
∴
| DK |
| CE |
| BK |
| BC |
| 1 |
| CE |
| BK |
| BC•DK |
同理可求:
| 1 |
| BF |
| CG |
| BC•DG |
| 1 |
| CE |
| 1 |
| BF |
| BK |
| BC•DK |
| CG |
| BC•DG |
∵DG=DK=
| 1 |
| 2 |
∴
| 1 |
| CE |
| 1 |
| BF |
| 2(BK+CG) |
| a2 |
又∵BK+CG=(BK+CK)+GK=a+
| 1 |
| 2 |
| 3 |
| 2 |
∴
| 1 |
| CE |
| 1 |
| BF |
| 3a |
| a2 |
| 3 |
| a |
即
| 1 |
| CE |
| 1 |
| BF |
| 3 |
| AB |

点评:考查了等边三角形的性质、相似三角形的性质及其应用问题;解题的关键是首先构造出两对相似三角形,然后利用相似三角形的性质列出有关比例式化简运算.

练习册系列答案
相关题目
 有理数a,b,c在数轴上的位置如图所示,下列各式成立的是( )
有理数a,b,c在数轴上的位置如图所示,下列各式成立的是( )| A、c>b>a |
| B、|a|>|b|>|c| |
| C、|c|>|b|>|a| |
| D、|c|>|a|>|b| |
下列等式中,是一元一次方程的有( )
①2013+4x=2014;②3x-2x=100;③2x+6y=15;④3x2-5x+26=0.
①2013+4x=2014;②3x-2x=100;③2x+6y=15;④3x2-5x+26=0.
| A、1个 | B、2个 | C、3个 | D、4个 |
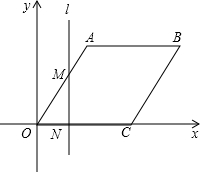 如图,在平面直角坐标系中,OA∥CB,AB∥OC,∠AOC=60°,OC=OA=4;
如图,在平面直角坐标系中,OA∥CB,AB∥OC,∠AOC=60°,OC=OA=4;