题目内容

18．已知a，b，c为△ABC的三条边，若a2+b2+c2=ab+ac+bc，则该△ABC是什么三角形？

分析 把a2+b2+c2=ab+ac+bc的两边乘2，然后分类利用完全平方公式各自因式分解，进一步利用非负数的性质得出a、b、c三边之间的关系解决问题．

解答 解：∵a2+b2+c2-ab-ac-bc=0，
∴2a2+2b2+2c2-2ab-2ac-2bc=0
∴a2+b2-2ab+b2+c2-2bc+a2+c2-2ac=0，
即（a-b）2+（b-c）2+（a-c）2=0
∴a-b=0，b-c=0，a-c=0，
∴a=b=c，
∴△ABC是等边三角形．

点评 此题考查利用完全平方公式因式分解和非负数的性质解决问题，要根据所给的条件灵活运用．

练习册系列答案
相关题目
8．关于x的一元一次方程4x+m+1=2x-1的解是负数，求m的取值范围．
9．已知A、B、C三点在同一直线上，且线段AB=8，BC=6，点D是线段AC的中点，求线段AD的长．
6．如图，平面直角坐标系中，每个小正方形边长都是1．
（1）按要求作图：①△ABC关于原点O逆时针旋转90°得到△A1B1C1；②△A1B1C1关于原点中心对称的△A2B2C2．
（2）写出A2、B2C2坐标，并求△A2B2C2的周长．
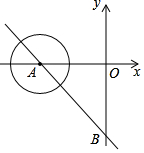13．如图，在直角坐标系中直线AB分别交x轴，y轴与A（-6，0）、B（0，-8）两点，现有一半径为1的动圆，圆心由A点，沿着AB方向以每秒1个单位的速度做平移运动，则经过几秒后动圆与坐标轴相切．
3．解方程：
（1）3x-2=1-2（x+1）
（2）$\frac{0.3x+0.5}{0.2}$-$\frac{2x-1}{3}$=1．
10．已知O为直线AB上的一点，∠COE是直角，OF平分∠AOE．
（1）如图1，若∠COF=28°，则∠BOE=56°；若∠COF=n°，则∠BOE=2n；∠BOE与∠COF的数量关系为∠BOE=2∠COF．
（2）当射线OE绕点O逆时针旋转到如图2的位置时，（1）中∠BOE与∠COF的关系是否仍然成立？如成立，请说明理由．
（3）在图3中，若∠COF=65°，在∠BOE的内部是否存在一条射线OD，使得2∠BOD+∠AOF=$\frac{1}{2}$（∠BOE-∠BOD）？若存在，请求出∠BOD的度数；若不存在，请说明理由．
7．图1是由若干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=$\frac{n（n+1）}{2}$．
如果图3中的圆圈共有13层．
（1）我们自上往下，在每个圆圈中都图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是79；
（2）我们自上往下，在每个圆圈中按图4的方式填上一串连续的整数-23，-22，-21，-20，…，求最底层最右边圆圈内的数是67；
（3）求图4中所有圆圈中各数值之和．（写出计算过程）
8．将如图中的图形折叠起来围成一个正方体，可以得到（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网