题目内容
11. 如图,在△ABC中,∠CAB=62°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为56°.
如图,在△ABC中,∠CAB=62°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为56°.
分析 先根据平行线的性质得∠ACC′=∠CAB=62°,再根据旋转的性质得∠CAC′等于旋转角,AC=AC′,则利用等腰三角形的性质得∠ACC′=∠AC′C=62°,然后根据三角形内角和定理可计算出∠CAC′的度数,从而得到旋转角的度数.
解答 解:∵CC′∥AB,
∴∠ACC′=∠CAB=62°
∵△ABC在平面内绕点A旋转到△AB′C′的位置,
∴∠CAC′等于旋转角,AC=AC′,
∴∠ACC′=∠AC′C=62°,
∴∠CAC′=180°-∠ACC′-∠AC′C=180°-2×62°=56°,
∴旋转角为56°.
故答案为56°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 两个等边三角形一定全等 | B. | 面积相等的两个三角形全等 | ||
| C. | 形状相同的两个三角形全等 | D. | 全等三角形的面积一定相等 |
6.一条船沿南偏西50°方向航行到某地,然后沿原航线返回,返回时的航行方向是( )
| A. | 南偏东50° | B. | 南偏西50° | C. | 北偏东50° | D. | 北偏西50° |
3. 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )
如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )
 如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )
如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=30°,则∠EAC的度数是( )| A. | 35° | B. | 40° | C. | 25° | D. | 30° |
20.在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共20只,某学习小组作摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表示活动进行中的一组统计数据:
请估算口袋中白球约是( )只.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
| A. | 8 | B. | 9 | C. | 12 | D. | 13 |
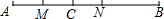 如图,线段AC=6,线段BC=9,点M是AC的中点,N在线段BC上,切$\frac{CN}{NB}$=$\frac{1}{2}$,则线段MN的长是( )
如图,线段AC=6,线段BC=9,点M是AC的中点,N在线段BC上,切$\frac{CN}{NB}$=$\frac{1}{2}$,则线段MN的长是( ) 在平面直角坐标系xOy中,抛物线y=ax2-3ax+c与x轴交于A(-1,0)、B两点(A点在B点左侧),与y轴交于点C(0,2).
在平面直角坐标系xOy中,抛物线y=ax2-3ax+c与x轴交于A(-1,0)、B两点(A点在B点左侧),与y轴交于点C(0,2).