题目内容
19.已知反比例函数y=$\frac{3k+1}{x}$的图象的两支分别在第二、四象限内,那么k的取值范围是( )| A. | k>-$\frac{1}{3}$ | B. | k>$\frac{1}{3}$ | C. | k<-$\frac{1}{3}$ | D. | k<$\frac{1}{3}$ |
分析 先根据函数y=$\frac{3k+1}{x}$的图象分别位于第二、四象限列出关于k的不等式,求出k的取值范围即可.
解答 解:∵函数y=$\frac{3k+1}{x}$的图象分别位于第二、四象限,
∴3k+1<0,
解得k<-$\frac{1}{3}$
故选:C.
点评 本题考查的是反比例函数的性质,熟知反比例函数y=$\frac{k}{x}$(k≠0)中,当k<0时,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知关于x的不等式x<2x-3的解可以使不等式x+2(x-3)>m成立,则m的取值范围是( )
| A. | m≤3 | B. | m<3 | C. | m≥3 | D. | m<-3 |
7. 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )
 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
8. 下面几何体的左视图为( )
下面几何体的左视图为( )
 下面几何体的左视图为( )
下面几何体的左视图为( )| A. |  | B. |  | C. |  | D. |  |
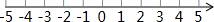 利用数轴,解一元一次不等式组:$\left\{\begin{array}{l}{x+4≤3(x+2)}\\{\frac{x-1}{2}<\frac{x}{3}}\end{array}\right.$.
利用数轴,解一元一次不等式组:$\left\{\begin{array}{l}{x+4≤3(x+2)}\\{\frac{x-1}{2}<\frac{x}{3}}\end{array}\right.$. 如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.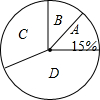 京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.
京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台. 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.