题目内容
1.已知在平面直角坐标系中,点P(4,-2)是双曲线y=$\frac{k}{x}$(k≠0)上的一个点,此双曲线与直线y=-2x交于A、B两点.(1)求A、B两点的坐标;
(2)在x轴的负半轴上找一点,使点A、B、C构成以AB为斜边的直角三角形,并求△ABC的面积.
分析 (1)先把点P(4,-2)代入y=$\frac{k}{x}$(k≠0)得到k=-8,从而确定双曲线的解析式,然后联立方程,解方程即可求得A、B的坐标;
(2)根据勾股定理求得OA=OB=2$\sqrt{5}$,因为在x轴的负半轴上找一点C,使点A、B、C构成以AB为斜边的直角三角形,则C点是以AB为直径的圆与x轴的负半轴的交点,所以OC=OA=OB=2$\sqrt{5}$,最后根据S△ABC=S△AOC+S△BOC即可求得.
解答 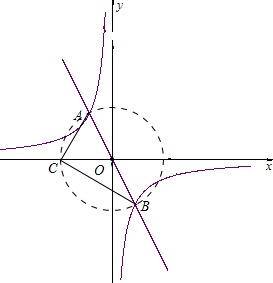 解:(1)把P(4,-2)代入y=$\frac{k}{x}$得k=-2×4=-8,
解:(1)把P(4,-2)代入y=$\frac{k}{x}$得k=-2×4=-8,
所以双曲线的解析式为y=-$\frac{8}{x}$,
解$\left\{\begin{array}{l}{y=-\frac{8}{x}}\\{y=-2x}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=-4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$,
所以A、B两点的坐标为(2,-4)和(-2,4);
(2)∵A、B两点的坐标为(2,-4)和(-2,4),
∴OA=OB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
在x轴的负半轴上找一点C,使点A、B、C构成以AB为斜边的直角三角形,则C点是以AB为直径的圆与x轴的负半轴的交点,如图,
∴OC=OA=OB=2$\sqrt{5}$,
∴S△ABC=S△AOC+S△BOC=$\frac{1}{2}$×2$\sqrt{5}$×4+$\frac{1}{2}$×2$\sqrt{5}$×4=8$\sqrt{5}$.
点评 本题考查了反比例函数和一次函数的问题:反比例函数与一次函数图象的交点坐标满足两函数的解析式.也考查了勾股定理和三角形的面积.

 在创建国家卫生城市环境综合整治行动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:
在创建国家卫生城市环境综合整治行动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:| 粉刷面积x(m2) | 100 | 200 | 300 | 400 | … |
| 费用y(元) | 2000 | 4000 | 6000 | 8000 | … |
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(x≥100)(m2)满足的函数关系式;
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为800m2,则选择哪家装饰公司进行施工更合算?
 如图.一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象 相交于A、B两点.
如图.一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象 相交于A、B两点. 如图,⊙O的直径AB=8cm,D为⊙O上一点,过点D的切线与AB的延长线于点C.AD=CD,求:
如图,⊙O的直径AB=8cm,D为⊙O上一点,过点D的切线与AB的延长线于点C.AD=CD,求: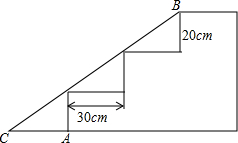 如图,新江公园入口处原有三级台阶,每级台阶高20cm,深为30cm,为了方便残疾人,拟将台阶改为斜坡,设台阶的起始点为A,斜坡的起始点为C,现将斜坡BC的坡比定为1:8,求AC和BC的长.
如图,新江公园入口处原有三级台阶,每级台阶高20cm,深为30cm,为了方便残疾人,拟将台阶改为斜坡,设台阶的起始点为A,斜坡的起始点为C,现将斜坡BC的坡比定为1:8,求AC和BC的长.