题目内容
13.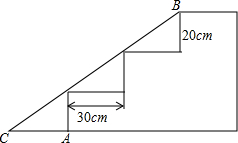 如图,新江公园入口处原有三级台阶,每级台阶高20cm,深为30cm,为了方便残疾人,拟将台阶改为斜坡,设台阶的起始点为A,斜坡的起始点为C,现将斜坡BC的坡比定为1:8,求AC和BC的长.
如图,新江公园入口处原有三级台阶,每级台阶高20cm,深为30cm,为了方便残疾人,拟将台阶改为斜坡,设台阶的起始点为A,斜坡的起始点为C,现将斜坡BC的坡比定为1:8,求AC和BC的长.
分析 首先过点B作BD⊥AC于D,根据题意即可求得AD与BD的长,然后由斜坡BC的坡度i=1:8,求得AC、CD的长,根据勾股定理求得答案.
解答 解:过点B作BD⊥AC于D,
AD=2×30=60(cm),BD=20×3=60(cm),
∵斜坡BC的坡度i=1:8,
∴BD:CD=1:8,
∴CD=8BD=8×60=480(cm),
∴AC=CD-AD=480-60=420(cm).
∴AC的长度是420cm,
则BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=300$\sqrt{2}$cm.
点评 此题考查了解直角三角形的应用-坡度问题,掌握坡度的定义,注意数形结合思想的应用与辅助线的作法是解题的关键.

练习册系列答案
相关题目