题目内容
20.写出一个二元一次方程组,使它的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,该方程组可以是$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$.分析 所谓“方程组”的解,指的是该数值满足方程组中的每一方程.在求解时,应先围绕$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,列一组算式,如2+(-1)=1,2-(-1)=3,然后用x,y代换,得 $\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$(答案不唯一).
解答 解:由2+(-1)=1,2-(-1)=3得:$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$(答案不唯一).
故答案为:$\left\{\begin{array}{l}{x+y=1}\\{x-y=3}\end{array}\right.$(答案不唯一).
点评 此题考查的知识点是二元一次方程组的解,本题是开放题,注意方程组的解的定义.围绕解列不同的算式即可列不同的方程组.

练习册系列答案
相关题目
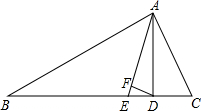 如图,在△ABC中,∠B=25°,∠C=65°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE.
如图,在△ABC中,∠B=25°,∠C=65°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE. (1)如图(1),求证:∠AOB=∠A+∠B+∠C;
(1)如图(1),求证:∠AOB=∠A+∠B+∠C;