题目内容
12. (1)如图(1),求证:∠AOB=∠A+∠B+∠C;
(1)如图(1),求证:∠AOB=∠A+∠B+∠C;(2)如图(2),请利用(1)中的结论求∠A+∠B+∠C+∠D+∠E+∠F的度数.
分析 (1)连接AB,利用三角形的内角和定理得出∠ABC+∠BAC+∠C=180,∠AOB=180°-∠OAB-∠OBA,进一步把∠OAB=∠BAC-∠A,∠OBA=∠ABC-∠B代换即可求得答案.
(2)根据三角形外角的性质,可得∠1与∠B、∠F的关系,∠2与∠A、∠E的关系,再根据多边形的内角和公式,可得答案.
解答 证明:(1)连接AB,如图(1)
∵∠ABC+∠BAC+∠C=180,∠AOB=180°-∠OAB-∠OBA,∠OAB=∠BAC-∠CAO,∠OBA=∠ABC-∠CBO,
∴∠AOB=180°-∠OAB-∠OBA
=180°-(∠ABC-∠CAO)-(∠BAC-∠CBO)
=180°-∠ABC-∠BAC+∠CAO+∠CBO=∠CAO+∠CBO+∠C;
(2)如图(2),
由三角形的外角等于与它不相邻的两个内角的和,得∠1=∠B+∠F,∠2=∠A+∠E,
由四边形内角和得∠1+∠2+∠D+∠E=(4-2)×180°=360°.
则∠A+∠B+∠C+∠D+∠E+∠F=360°.
点评 此题考查三角形的内角和,角的和与差,掌握三角形的内角和定理是解决问题的关键.

练习册系列答案
相关题目
4.等腰三角形的一个内角等于40°,则它两底角的平分线所夹的钝角为( )
| A. | 110° | B. | 140° | C. | 110°或140° | D. | 100°或120° |
 如图,已知∠B=∠C,AD=AE,请说明AB与AC相等.
如图,已知∠B=∠C,AD=AE,请说明AB与AC相等.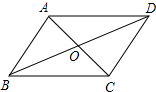 如图,在四边形ABCD中,AB=CD,AD=BC,AC与BD相交于O点,则由“SSS”可判定( )对三角形全等.
如图,在四边形ABCD中,AB=CD,AD=BC,AC与BD相交于O点,则由“SSS”可判定( )对三角形全等.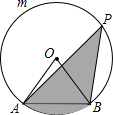 如图,AB是⊙O的弦,AB=2,点P在$\widehat{AmB}$上运动,且∠APB=30°.
如图,AB是⊙O的弦,AB=2,点P在$\widehat{AmB}$上运动,且∠APB=30°.