题目内容
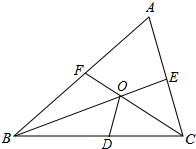 如图,在△ABC中,∠A=60°,∠ABC的平分线BE和∠ACB的平分线CF相交于点O.
如图,在△ABC中,∠A=60°,∠ABC的平分线BE和∠ACB的平分线CF相交于点O.(1)求∠BOF的度数;
(2)若点D在BC上,且BD=BF,求证:OF=OD=OE.
考点:全等三角形的判定与性质
专题:
分析:(1)根据三角形的内角和定理,可得出∠ABC+∠ACB=120°,由角平分线的定义可得出∠OBC+∠OCB=60°,再根据外角的性质得出∠BOF的度数;
(2)根据SAS证明△BOD≌△BOF,得出OD=OF,再根据ASA证明△COD≌△COE,得出OD=OE,从而得出OF=OD=OE.
(2)根据SAS证明△BOD≌△BOF,得出OD=OF,再根据ASA证明△COD≌△COE,得出OD=OE,从而得出OF=OD=OE.
解答:
解:(1)∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵∠ABC的平分线BE和∠ACB的平分线CF相交于点O,
∴∠ABC=2∠OBD,∠ACB=2∠OCB,
∴∠BOF=∠OBC+∠OCB=
(∠ABC+∠ACB)=60°;
(2)在△BOD和△BOF中,
,
∴△BOD≌△BOF(SAS),
∴OD=OF,∠BOD=∠BOF=60°,
∵∠COD=∠COE=60°,
在△COD和△COE中,
,
∴△COD≌△COE(ASA),
∴OD=OE,
∴OD=OE=OF.
∴∠ABC+∠ACB=120°,
∵∠ABC的平分线BE和∠ACB的平分线CF相交于点O,
∴∠ABC=2∠OBD,∠ACB=2∠OCB,
∴∠BOF=∠OBC+∠OCB=
| 1 |
| 2 |
(2)在△BOD和△BOF中,
|
∴△BOD≌△BOF(SAS),
∴OD=OF,∠BOD=∠BOF=60°,
∵∠COD=∠COE=60°,
在△COD和△COE中,
|
∴△COD≌△COE(ASA),
∴OD=OE,
∴OD=OE=OF.
点评:本题考查了全等三角形的判定和性质,涉及的知识点有:全等三角形的判定、性质,判定的方法:SSS、SAS、ASA/AAS、HL.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在-2、-2012、0、0.1这四个数中,最大的数是( )
| A、-2 | B、-2012 |
| C、0 | D、0.1 |
 如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD等于( )cm.
如图,AB是⊙O的直径,OD⊥AC于点D,BC=6cm,则OD等于( )cm.| A、2 | B、3 | C、4 | D、5 |
若a>b,且c为实数,则( )
| A、ac>bc |
| B、ac<bc |
| C、ac2>bc2 |
| D、ac2≥bc2 |
 x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 .
x2交于点Q,则图中阴影部分的面积为 .
 如图,在方格纸内将△ABC水平向右平移5个单位得到△A′B′C′.
如图,在方格纸内将△ABC水平向右平移5个单位得到△A′B′C′. 如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若
如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若