题目内容
7. 如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为2a,2b,点A,D,G在y轴上,坐标原点O为AD的中点,抛物线y=mx2过C,F两点,连接FD并延长交抛物线于点M.
如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为2a,2b,点A,D,G在y轴上,坐标原点O为AD的中点,抛物线y=mx2过C,F两点,连接FD并延长交抛物线于点M.(1)若a=1,求m和b的值;
(2)求$\frac{b}{a}$的值;
(3)判断以FM为直径的圆与AB所在直线的位置关系,并说明理由.
分析 (1)由a=1,根据正方形的性质及已知条件得出C(2,1).将C点坐标代入y=mx2,求出m=$\frac{1}{4}$,则抛物线解析式为y=$\frac{1}{4}$x2,再将F(2b,2b+1)代入y=$\frac{1}{4}$x2,即可求出b的值;
(2)由正方形ABCD的边长为2a,坐标原点O为AD的中点,得出C(2a,a).将C点坐标代入y=mx2,求出m=$\frac{1}{4a}$,则抛物线解析式为y=$\frac{1}{4a}$x2,再将F(2b,2b+a)代入y=$\frac{1}{4a}$x2,整理得出方程b2-2ab-a2=0,把a看作常数,利用求根公式得出b=(1±$\sqrt{2}$)a(负值舍去),那么$\frac{b}{a}$=1+$\sqrt{2}$;
(3)先利用待定系数法求出直线FD的解析式为y=x+a.再求出M点坐标为(2a-2$\sqrt{2}$a,3a-2$\sqrt{2}$a).又F(2a+2$\sqrt{2}$a,3a+2$\sqrt{2}$a),利用中点坐标公式得到以FM为直径的圆的圆心O′的坐标为(2a,3a),再求出O′到直线AB(y=-a)的距离d的值,以FM为直径的圆的半径r的值,由d=r,根据直线与圆的位置关系可得以FM为直径的圆与AB所在直线相切.
解答 解:(1)∵a=1,
∴正方形ABCD的边长为2,
∵坐标原点O为AD的中点,
∴C(2,1).
∵抛物线y=mx2过C点,
∴1=4m,解得m=$\frac{1}{4}$,
∴抛物线解析式为y=$\frac{1}{4}$x2,
将F(2b,2b+1)代入y=$\frac{1}{4}$x2,
得2b+1=$\frac{1}{4}$×(2b)2,b=1±$\sqrt{2}$(负值舍去).
故m=$\frac{1}{4}$,b=1+$\sqrt{2}$;
(2)∵正方形ABCD的边长为2a,坐标原点O为AD的中点,
∴C(2a,a).
∵抛物线y=mx2过C点,
∴a=m•4a2,解得m=$\frac{1}{4a}$,
∴抛物线解析式为y=$\frac{1}{4a}$x2,
将F(2b,2b+a)代入y=$\frac{1}{4a}$x2,
得2b+a=$\frac{1}{4a}$×(2b)2,
整理得b2-2ab-a2=0,
解得b=(1±$\sqrt{2}$)a(负值舍去),
∴$\frac{b}{a}$=1+$\sqrt{2}$;
(3)以FM为直径的圆与AB所在直线相切.理由如下:
∵D(0,a),
∴可设直线FD的解析式为y=kx+a,
∵F(2b,2b+a),
∴2b+a=k•2b+a,解得k=1,
∴直线FD的解析式为y=x+a.
将y=x+a代入y=$\frac{1}{4a}$x2,
得x+a=$\frac{1}{4a}$x2,解得x=2a±2$\sqrt{2}$a(正值舍去),
∴M点坐标为(2a-2$\sqrt{2}$a,3a-2$\sqrt{2}$a).
∵F(2b,2b+a),b=(1+$\sqrt{2}$)a,
∴F(2a+2$\sqrt{2}$a,3a+2$\sqrt{2}$a),
∴以FM为直径的圆的圆心O′的坐标为(2a,3a),
∴O′到直线AB(y=-a)的距离d=3a-(-a)=4a,
∵以FM为直径的圆的半径r=O′F=$\sqrt{(2a+2\sqrt{2}a-2a)^{2}+(3a+2\sqrt{2}a-3a)^{2}}$=4a,
∴d=r,
∴以FM为直径的圆与AB所在直线相切.
点评 本题是二次函数的综合题型,其中涉及到正方形的性质,待定系数法求二次函数、一次函数的解析式,一元二次方程的求根公式,直线与抛物线交点坐标的求法,直线与圆的位置关系.综合性较强,难度适中.正确求出抛物线的解析式是解题的关键.

| A. |  | B. |  | C. |  | D. |  |
| A. | 2个 | B. | 4个 | C. | 5个 | D. | 6个 |
| A. | a3•b3=(ab)3 | B. | a2•a3=a6 | C. | a6÷a3=a2 | D. | (a2)3=a5 |






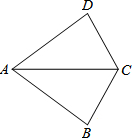 如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是DC=BC或∠DAC=∠BAC.
如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加的一个条件可以是DC=BC或∠DAC=∠BAC. 如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为14.
如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为14.