题目内容
17. 如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为14.
如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为14.
分析 运用平移的观点,五个小矩形的上边之和等于AD,下边之和等于BC,同理,它们的左边之和等于AB,右边之和等于DC,可知五个小矩形的周长之和为矩形ABCD的周长.
解答 解:将五个小矩形的所有上边平移至AD,所有下边平移至BC,所有左边平移至AB,所有右边平移至CD,
则五个小矩形的周长之和=2(AB+BC)=2×(3+4)=14.
故答案为:14.
点评 本题考查了平移的性质,矩形性质的运用.关键是运用平移的观点,将小矩形的四边平移,与大矩形的周长进行比较.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
5.已知x=1,y=2,则代数式x-y的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -3 |
12.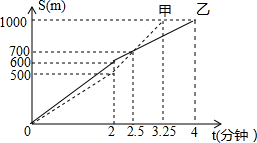 甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )
甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )
 甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )
甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法错误的是( )| A. | 甲、乙两人进行1000米赛跑 | |
| B. | 甲先慢后快,乙先快后慢 | |
| C. | 比赛到2分钟时,甲、乙两人跑过的路程相等 | |
| D. | 甲先到达终点 |
9.关于反比例函数y=-$\frac{2}{x}$,下列说法正确的是( )
| A. | 图象过(1,2)点 | B. | 图象在第一、三象限 | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 当x<0时,y随x的增大而增大 |
6.下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,正确的是( )
| A. | 没有交点 | B. | 只有一个交点,且它位于y轴右侧 | ||
| C. | 有两个交点,且它们均位于y轴左侧 | D. | 有两个交点,且它们均位于y轴右侧 |
 如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为2a,2b,点A,D,G在y轴上,坐标原点O为AD的中点,抛物线y=mx2过C,F两点,连接FD并延长交抛物线于点M.
如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为2a,2b,点A,D,G在y轴上,坐标原点O为AD的中点,抛物线y=mx2过C,F两点,连接FD并延长交抛物线于点M. 如图,在?ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
如图,在?ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF. 图中是对顶角量角器,用它测量角的原理是对顶角相等.
图中是对顶角量角器,用它测量角的原理是对顶角相等.