题目内容
16.在平面直角坐标系中,点A的坐标为(m,n),若点A′(m,n′)的纵坐标满足n′=$\left\{\begin{array}{l}m-n(m≥n)\\ n-m(n>m)\end{array}$,则称点A′是点A的“绝对点”.(1)点(1,2)的“绝对点”的坐标为(1,1).
(2)点P是函数y=$\frac{2}{x}$的图象上的一点,点P′是点P的“绝对点”.若点P与点P′重合,求点P的坐标.
(3)点Q(a,b)的“绝对点”Q′是函数y=2x2的图象上的一点.当0≤a≤2 时,求线段QQ′的最大值.
分析 (1)根据“绝对点”的定义求解可得;
(2)设点P的坐标为(m,n).若m≥n,则P′的坐标为(m,m-n),根据P与P′重合知n=m-n,由mn=2求得m、n的值可得;若m<n,则P′的坐标为(m,n-m).可得m=0,舍去;
(3)当a≥b时,Q′的坐标为(a,a-b),由Q′是函数y=2x2的图象上一点知a-b=2a2,即b=a-2a 2.可得QQ′=|a-b-b|=|a-2(a-2a2)|=|4a2-a|,利用二次函数的图象和性质求出其最大值;当a<b时,Q′的坐标为(a,b-a),知QQ′=|b-b+a|=|a|,显然可得其最值.
解答 解:(1)∵2>1,
∴点(1,2)的“绝对点”的纵坐标为2-1=1,
则点(1,2)的“绝对点”的坐标为(1,1),
故答案为:(1,1).
(2)设点P的坐标为(m,n).
当m≥n时,P′的坐标为(m,m-n).
若P与P′重合,则n=m-n,
又mn=2.
所以n=±1.
即P的坐标为(2,1)或(-2,-1).
又(-2,-1)不符合题意,舍去,
所以P的坐标为(2,1).
当m<n时,P′的坐标为(m,n-m).可得m=0,舍去.
综上所述,点P的坐标为(2,1).
(3)当a≥b时,Q′的坐标为(a,a-b).
因为Q′是函数y=2x2的图象上一点,
所以a-b=2a2.
即b=a-2a 2.
QQ′=|a-b-b|=|a-2(a-2a2)|=|4a2-a|,
其函数图象如图所示: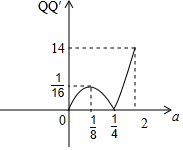 .
.
由图象可知,当a=2时,QQ′的最大值为14.
当a<b时,Q′的坐标为(a,b-a).
QQ′=|b-b+a|=|a|.
当a=2时,QQ′的最大值为2.
综上所述,Q Q′的最大值为14或2.
点评 本题主要考查二次函数的综合应用,理解“绝对点”的定义及二次函数的图象和性质、两点间的距离公式是解题的关键.

 如图,AB∥CD,AD与BC交于点E,若∠B=35°,∠D=45°,则∠AEC=( )
如图,AB∥CD,AD与BC交于点E,若∠B=35°,∠D=45°,则∠AEC=( )| A. | 35° | B. | 45° | C. | 70° | D. | 80° |
 如图,正五边形ABCDE中.
如图,正五边形ABCDE中. 已知:如图,AD=BC,AC=BD.求证:∠OCD=∠ODC.
已知:如图,AD=BC,AC=BD.求证:∠OCD=∠ODC. 如图,直线a∥b,直线c与a、b均相交.如果∠1=50°,那么∠2的度数是130°.
如图,直线a∥b,直线c与a、b均相交.如果∠1=50°,那么∠2的度数是130°. 如图,已知△ABC.
如图,已知△ABC.