题目内容
5.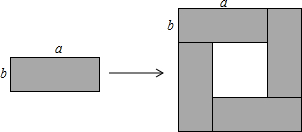 如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | 4ab=(a+b)2-(a-b)2 | D. | (a+b)(a-b)=a2-b2 |
分析 根据图形的组成以及正方形和长方形的面积公式,知:大正方形的面积-小正方形的面积=4个矩形的面积.
解答 解:∵大正方形的面积-小正方形的面积=4个矩形的面积,
∴(a+b)2-(a-b)2=4ab,即4ab=(a+b)2-(a-b)2.
故选C.
点评 考查了完全平方公式的几何背景,能够正确找到大正方形和小正方形的边长是难点.解决问题的关键是读懂题意,找到所求的量的等量关系.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
16. 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3\sqrt{13}}{13}$ | D. | $\frac{4\sqrt{13}}{13}$ |
20.25的平方根是( )
| A. | ±5 | B. | -5 | C. | 5 | D. | 25 |
10.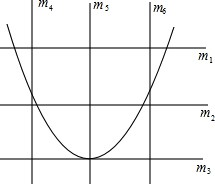 王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )
王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )
 王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )
王芳将如图所示的三条水平直线m1,m2,m3的其中一条记为x轴(向右为正方向),三条竖直直线m4,m5,m6的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了抛物线y=ax2-6ax-3,则她所选择的x轴和y轴分别为( )| A. | m1,m4 | B. | m2,m3 | C. | m3,m6 | D. | m4,m5 |
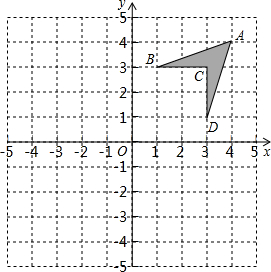 如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1)
如图,在平面直角坐标系中,将四边形ABCD称为“基本图形”,且各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1)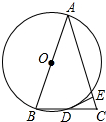 如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.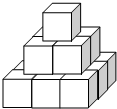 如图把14个棱长为1分米的正方体摆放在课桌上,现在想露出的表面都涂上颜色,则涂上颜色部分的面积为33平方分米.
如图把14个棱长为1分米的正方体摆放在课桌上,现在想露出的表面都涂上颜色,则涂上颜色部分的面积为33平方分米.