题目内容
 根据数轴上a,b,c的大小关系,化简|a+b|+|b+c|-|a-c|.
根据数轴上a,b,c的大小关系,化简|a+b|+|b+c|-|a-c|.考点:整式的加减,数轴,绝对值
专题:计算题
分析:根据数轴表示数的方法得到a>0,b<0,c<0,且|b|>|c|>|a|,再利用绝对值的意义去绝对值得到原式|=-(a+b)-(b+c)-(a-c),然后去括号后合并即可.
解答:解:根据题意得a>0,b<0,c<0,且|b|>|c|>|a|,
所以|a+b|+|b+c|-|a-c|=-(a+b)-(b+c)-(a-c)
=-a-b-b-c-a+c
=-2a-2b.
所以|a+b|+|b+c|-|a-c|=-(a+b)-(b+c)-(a-c)
=-a-b-b-c-a+c
=-2a-2b.
点评:本题考查了整式的加减:几个整式相加减,通常用括号把每一个整式括起来,再用加减号连接;然后去括号、合并同类项.整式的加减实质上就是合并同类项.注意去绝对值后符合的变化.

练习册系列答案
相关题目
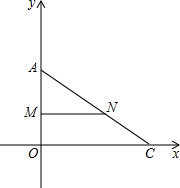 如图,平面直角坐标系中,点A,C两点分别在x轴和y轴上,点A的坐标点(0,6),点C的坐标(8,0),M、N分别为OA、AC的中点,动点P从O出发以每秒1个单位的速度沿折线OCNM运动,以P为圆心,以3为半径作⊙P,以N为圆心,以1为半径作⊙N.
如图,平面直角坐标系中,点A,C两点分别在x轴和y轴上,点A的坐标点(0,6),点C的坐标(8,0),M、N分别为OA、AC的中点,动点P从O出发以每秒1个单位的速度沿折线OCNM运动,以P为圆心,以3为半径作⊙P,以N为圆心,以1为半径作⊙N.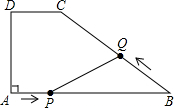 如图在梯形ABCD中,DC∥AB,∠A=90°,AD=6厘米,DC=4厘米,AD:BC=3:5,动点P从A出发以2厘米/秒的速度沿AB方向向点B运动,动点Q从点B出发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒.
如图在梯形ABCD中,DC∥AB,∠A=90°,AD=6厘米,DC=4厘米,AD:BC=3:5,动点P从A出发以2厘米/秒的速度沿AB方向向点B运动,动点Q从点B出发以3厘米/秒的速度沿B?C?D方向向点D运动,两个动点同时出发,当其中一个动点到达终点时,另一个动点也随之停止.设动点运动的时间为t秒. 在Rt△ABC中,AC=BC,∠ACB=90°,D为AB上一点,连结DC,将DC绕点C顺时针旋转90°,使D点与E点重合,连结DE,探究AD、BD、DE之间的关系并证明.
在Rt△ABC中,AC=BC,∠ACB=90°,D为AB上一点,连结DC,将DC绕点C顺时针旋转90°,使D点与E点重合,连结DE,探究AD、BD、DE之间的关系并证明.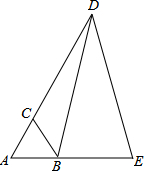 如图,等边△ABC,D、E分别在AC、AB的延长线上,且CD=AE,求证:BD=DE.
如图,等边△ABC,D、E分别在AC、AB的延长线上,且CD=AE,求证:BD=DE. 如图,是一个很大很大的水域,现要测量A点和B点的距离,直接测量难度较大,你能设计一种简单的方法吗?请画图,写出已知、求证,并解释你的原理.
如图,是一个很大很大的水域,现要测量A点和B点的距离,直接测量难度较大,你能设计一种简单的方法吗?请画图,写出已知、求证,并解释你的原理.