题目内容
2.有性状、大小和质地都完全相同的3张卡片,正面分别写有字母A、B、C和一个算式或判断,将这3张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取另一张
(1)用画树状图法或列表法,求抽取的两张卡片可能出现A的概率(卡片可用A、B、C表示)
(2)若用实验的方法抽取两张卡片,请估计抽取的卡片中算式或判断都正确的概率;并请你说出一种模拟此实验的方法.
分析 (1)利用树状图展示所有6种等可能的结果数,找出抽取的两张卡片出现A的结果数,然后根据概率公式求解;
(2)利用概率公式可计算出抽取的卡片中算式或判断都正确的概率=$\frac{1}{3}$.可以设计模拟实验估计此概率:将这3张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取另一张,连续50次,记下卡片中算式或判断都正确的次数;再连续50次,记下卡片中算式或判断都正确的次数;接着连续50次,记下卡片中算式或判断都正确的次数,然后通过计卡片中算式或判断都正确的频率可估计抽取的卡片中算式或判断都正确的概率.
解答 解:(1)画树状图为:
共有6种等可能的结果数,其中抽取的两张卡片出现A的结果数为4,
所以抽取的两张卡片可能出现A的概率=$\frac{4}{6}$=$\frac{2}{3}$;
(2)共有6种等可能的结果数,其中抽取的两张卡片上算式或判断都正确的结果数为2,
所以抽取的卡片中算式或判断都正确的概率=$\frac{2}{6}$=$\frac{1}{3}$.
可以设计模拟实验:将这3张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取另一张,连续50次,记下卡片中算式或判断都正确的次数;再连续50次,记下卡片中算式或判断都正确的次数;
接着连续50次,记下卡片中算式或判断都正确的次数,然后统计出实验的总次数和卡片中算式或判断都正确的次数,再计算出卡片中算式或判断都正确的频率,于是可估计抽取的卡片中算式或判断都正确的概率.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
7. 如图,ABCD是一块长方形纸板.试画一条直线,将它的面积分成相等的两部分,那么这种直线能画( )
如图,ABCD是一块长方形纸板.试画一条直线,将它的面积分成相等的两部分,那么这种直线能画( )
 如图,ABCD是一块长方形纸板.试画一条直线,将它的面积分成相等的两部分,那么这种直线能画( )
如图,ABCD是一块长方形纸板.试画一条直线,将它的面积分成相等的两部分,那么这种直线能画( )| A. | 2条 | B. | 4条 | C. | 8条 | D. | 无数条 |
14.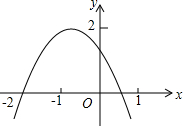 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③c<2;④b2>4ac.其中正确的有( )
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③c<2;④b2>4ac.其中正确的有( )
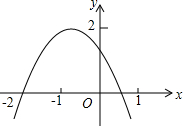 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③c<2;④b2>4ac.其中正确的有( )
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③c<2;④b2>4ac.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列函数中,自变量x的取值范围是x>-2的是( )
| A. | y=x+2 | B. | y=$\frac{1}{x+2}$ | C. | y=$\sqrt{x+2}$ | D. | y=$\frac{x-2}{\sqrt{x+2}}$ |
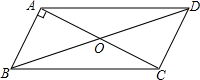 如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,则BD=2$\sqrt{2}$.
如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,则BD=2$\sqrt{2}$.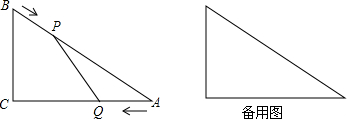
 如图,已知点O在直线AB上,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.
如图,已知点O在直线AB上,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.