题目内容
17. 如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.
如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.(1)图中有多少个小于180°的角?
(2)若OE平分∠BOC,求∠DOE的度数;
(3)若∠COE=2∠BOE,∠DOE=108°,求∠COE的度数.
分析 (1)根据角的定义,按照一定的规律计数即可;
(2)依据角平分线的定义可知$∠COD=\frac{1}{2}∠AOC$,$∠COE=\frac{1}{2}∠BOC$,然后逆用乘法的分配律可求得∠DOE=90°;
(3)设∠BOE=x,然后依据∠DOE=108°列方程求解即可.
解答 解:(1)图中小于180°的角有∠AOD、∠AOC、∠AOE、∠DOC、∠DOE、∠DOB、∠COE、∠COB、∠EOB共9个;
(2)∵OD平分∠AOC,OE平分∠BOC,
∴$∠COD=\frac{1}{2}∠AOC$,$∠COE=\frac{1}{2}∠BOC$.
∵∠AOC+∠BOC=180°,
∴$∠COD+∠COE=\frac{1}{2}∠AOC+\frac{1}{2}∠BOC=\frac{1}{2}(∠AOC+∠BOC)=90°$.
∴∠DOE=∠COD+∠COE=90°.
(3)设∠BOE=x,
∵∠COE=2∠BOE,∴∠COE=2x,
∴∠AOC=180°-3x.
∵OD平分∠AOC,
∴$∠COD=\frac{1}{2}∠AOC$.
∵∠COD+∠COE═∠DOE=108°,
∴$\frac{1}{2}(180°-3x)+2x=108°$,x=36°.
∴∠COE═72°.
点评 本题主要考查的是角的计算,依据图形间角的和差关系列出关于x的方程是解题的关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
7.在半径为6的⊙O中,120°圆心角所对的弧长是( )
| A. | π | B. | 2π | C. | 4π | D. | 6π |
12.下列等式中正确的是( )
| A. | -(a-b)=b-a | B. | -(a+b)=-a+b | C. | 2(a+1)=2a+1 | D. | -(3-x)=3+x |
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是3.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0,其中正确的个数是3.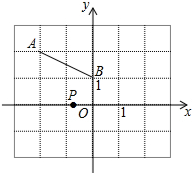 如图,直角坐标系中,点A(-2,2)、B(0,1),点P在x轴上,且△PAB是等腰三角形,则满足条件的点P共4 个.
如图,直角坐标系中,点A(-2,2)、B(0,1),点P在x轴上,且△PAB是等腰三角形,则满足条件的点P共4 个. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象写出一条此函数的性质对称轴为直线x=1(答案不唯一).
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象写出一条此函数的性质对称轴为直线x=1(答案不唯一).