题目内容
5.阅读理解.阅读下列材料:
老师提倡同学们自己出题,下面是王海同学出的两道题及解答过程:
题目1:已知(a-3)2+|b-1|=0,求a,b的值.
解:∵(a-3)2+|b-1|=0,
∴a-3=0,b-1=0.
∴a=3,b=1.
题目2:已知(a-3)2+|b-1|=1,求a,b的值.
解:∵(a-3)2+|b-1|=1,
∴(a-3)2=0,|b-1|=1或(a-3)2=1,|b-1|=0.
∴a=3,b=0;a=3,b=2;a=4,b=1;a=2,b=1.
老师说:“题目1的解答过程跳步了.题目2在编制时应该再添加已知条件”.
请阅读以上材料,解答下列问题:
(1)补全题目1的解答过程;
(2)依据题目2的解答过程,题目2中应添加的已知条件是:a、b为整数.
分析 (1)根据非负数的性质解答即可;
(2)根据整数的性质解答.
解答 解:(1)∵(a-3)2+|b-1|=0,
∴(a-3)2=0,|b-1|=0,
∴a-3=0,b-1=0.
∴a=3,b=1;
(2)题目2中应添加的已知条件是:a、b为整数,
故答案为:a、b为整数.
点评 本题考查的是非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
20.下列各式中,不成立的是( )
| A. | (-2)1=-21 | B. | (-2)2=-22 | C. | (-2)2=22 | D. | (-2)3=-23 |
15.下列各式中,正确的是( )
| A. | $\frac{x^6}{x^2}={x^3}$ | B. | $\frac{x+m}{x+n}=\frac{m}{n}$ | C. | $\frac{-a+b}{c}=-\frac{a+b}{c}$ | D. | $\frac{1}{a}+\frac{1}{b}=\frac{a+b}{ab}$ |
 如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.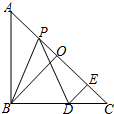 如图,在△ABC中,∠ABC=90°,AB=BC,AC=2a,点O是AC的中点,点P是AC的任意一点,点D在BC边上,且满足PB=PD,作DE⊥AC于点E,设DE=x.
如图,在△ABC中,∠ABC=90°,AB=BC,AC=2a,点O是AC的中点,点P是AC的任意一点,点D在BC边上,且满足PB=PD,作DE⊥AC于点E,设DE=x. 如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.
如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内. 如图,将一副三角板叠放在一起,使直角顶点重合于A,则∠BAC+∠EAD=180°.
如图,将一副三角板叠放在一起,使直角顶点重合于A,则∠BAC+∠EAD=180°.