题目内容
6.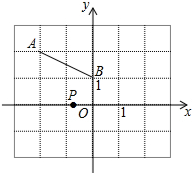 如图,直角坐标系中,点A(-2,2)、B(0,1),点P在x轴上,且△PAB是等腰三角形,则满足条件的点P共4 个.
如图,直角坐标系中,点A(-2,2)、B(0,1),点P在x轴上,且△PAB是等腰三角形,则满足条件的点P共4 个.
分析 由AB=AP,可得以A为圆心,AB为半径画圆,交x轴有二点P1(-1,0),P2(-3,0);
由BP=AB,可得以B为圆心,BA为半径画圆,交x轴有二点P3(-2,0),(2,0)不能组成△ABP,
由AP=BP,可得AB的垂直平分线交x轴一点P4(PA=PB).
解答 解:如图,点A(-2,2)、B(0,1),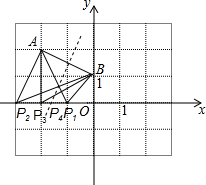
①以A为圆心,AB为半径画圆,交x轴有二点P1(-1,0),P2(-3,0),此时(AP=AB);
②以B为圆心,BA为半径画圆,交x轴有二点P3(-2,0),(2,0)不能组成△ABP,故舍去,此时(BP=AB);
③AB的垂直平分线交x轴一点P4(PA=PB),此时(AP=BP);
设此时P4(x,0),
则(x+2)2+4=x2+1,
解得:x=-$\frac{7}{4}$,
∴P4(-$\frac{7}{4}$,0).
∴符合条件的点有4个.
故答案为4.
点评 此题考查了等腰三角形的判定.此题那难度适中,注意掌握数形结合思想与分类讨论思想的应用.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
15.下列各式中,正确的是( )
| A. | $\frac{x^6}{x^2}={x^3}$ | B. | $\frac{x+m}{x+n}=\frac{m}{n}$ | C. | $\frac{-a+b}{c}=-\frac{a+b}{c}$ | D. | $\frac{1}{a}+\frac{1}{b}=\frac{a+b}{ab}$ |
 如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
如图,所有小正方形的边长都为1个单位,A、B、C均在格点上. 如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内.
如图,点O在直线AB上,OD是∠AOC的平分线,射线OE在∠BOC内. 如图,将一副三角板叠放在一起,使直角顶点重合于A,则∠BAC+∠EAD=180°.
如图,将一副三角板叠放在一起,使直角顶点重合于A,则∠BAC+∠EAD=180°.