题目内容
20. 已知抛物线y=ax2+bx+4在坐标系中的位置如图所示,它与x,y轴的交点分别为A(-1,0),B,P是其对称轴x=1上的动点,根据图中提供的信息,得出以下结论:
已知抛物线y=ax2+bx+4在坐标系中的位置如图所示,它与x,y轴的交点分别为A(-1,0),B,P是其对称轴x=1上的动点,根据图中提供的信息,得出以下结论:①2a+b=0,
②x=3是方程ax2+bx+4=0的一个根,
③△PAB周长的最小值是5+$\sqrt{17}$,
④9a+4<3b.
其中正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据对称轴方程求得a、b的数量关系;
②根据抛物线的对称性知抛物线与x轴的另一个交点的横坐标是3;
③利用两点间直线最短来求△PAB周长的最小值;
④根据图象知,当x=-3时,y<0,得到9a-3b+4<0,即9a+4<3b.
解答 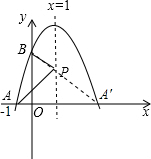 解:①根据图象知,对称轴是直线x=-$\frac{b}{2a}$=1,则b=-2a,即2a+b=0.
解:①根据图象知,对称轴是直线x=-$\frac{b}{2a}$=1,则b=-2a,即2a+b=0.
故①正确;
②根据图象知,点A的坐标是(-1,0),对称轴是x=1,则根据抛物线关于对称轴对称的性质知,抛物线与x轴的另一个交点的坐标是(3,0),所以x=3是ax2+bx+3=0的一个根,故②正确;
③如图所示,点A关于x=1对称的点是A′,即抛物线与x轴的另一个交点.
连接BA′与直线x=1的交点即为点P,
则△PAB周长的最小值是(BA′+AB)的长度.
∵A(-1,0),B(0,4),A′(3,0),
∴AB=$\sqrt{17}$,BA′=5.即△PAB周长的最小值是5+$\sqrt{17}$.
故③正确;
④根据图象知,当x=-3时,y<0,
∴9a-3b+4<0,即9a+4<3b,
故④正确.
综上所述,正确的结论是:①②③④.
故选D.
点评 本题考查的是二次函数综合题,涉及到二次函数图象与系数的关系,二次函数图象的性质以及两点之间直线最短.解答该题时,充分利用了抛物线的对称性.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
8.已知2是关于x的方程x2-2mx+3m=0的一个根,并且等腰三角形ABC的腰和底边长恰好是这个方程的两个根,则△ABC的周长为( )
| A. | 10 | B. | 14 | C. | 10或14 | D. | 8或10 |
10.用配方法解方程3x2-6x+2=0,则方程可变形为( )
| A. | (x-3)2=$\frac{2}{3}$ | B. | 3(x-1)2=$\frac{2}{3}$ | C. | (3x-1)2=1 | D. | (x-1)2=$\frac{1}{3}$ |
 如图,O是直线AB上一点,∠AOC=50°17′,则∠BOC=129°43′.
如图,O是直线AB上一点,∠AOC=50°17′,则∠BOC=129°43′.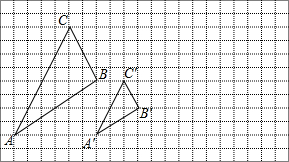 如图,△ABC 与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在正方形网格的格点上.
如图,△ABC 与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在正方形网格的格点上.
 已知:如图,AB∥CD,E是AB的中点,∠CEA=∠DEB.
已知:如图,AB∥CD,E是AB的中点,∠CEA=∠DEB. 如图,已知:∠ACB=∠ADC=90°,AD=2,CD=2,当AB的长为4时,△ACB与△ADC相似.
如图,已知:∠ACB=∠ADC=90°,AD=2,CD=2,当AB的长为4时,△ACB与△ADC相似.