题目内容
1.若方程(k-1)x2-$\sqrt{2-k}$x+$\frac{1}{4}$=0有两个实数根,则k的取值范围是k≤$\frac{3}{2}$且k≠1.分析 首先利用根的判别式△=b2-4ac≥0,根据一元二次方程的意义和二次根式的意义得出k-1≠0,2-k≥0,三者结合得出答案即可.
解答 解:∵方程(k-1)x2-$\sqrt{2-k}$x+$\frac{1}{4}$=0有两个实数根,
∴△=b2-4ac=2-k-k+1≥0,k≠1,2-k≥0,
解得:k≤$\frac{3}{2}$且k≠1.
故答案为:k≤$\frac{3}{2}$且k≠1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.以及一元二次方程的意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如图,移动小菱形◇可以得到美丽的“中国结”图案,如图三个图案是由小菱形◇平移后得到的类似“中国结”的图案,如果按图中的规律,那么第10个图案中,小菱形◇有( )
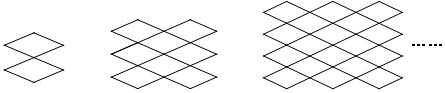

| A. | 62个 | B. | 162个 | C. | 184个 | D. | 200个 |
 ;
;