题目内容
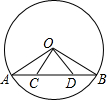如图，AB是⊙O的一条弦，线段OC、OD交弦AB于点C、D，且AC=BD．求证：OC=OD．考点：垂径定理
专题：证明题
分析：过点O作OE⊥AB于点E，由垂径定理可知AE=BE，再根据AC=BD可知CE=DE，根据SAS定理可得出△OAE≌△ODE，故可得出结论．
解答：
证明：过点O作OE⊥AB于点E，
∵OE⊥AB，
∴AE=BE．
∵AC=BD，
∴AE-AC=BE-BD，即CE=DE，
在△OAE与△ODE中，
∵
，
∴△OAE≌△ODE（SAS），
∴OC=OD．
证明：过点O作OE⊥AB于点E，∵OE⊥AB，
∴AE=BE．
∵AC=BD，
∴AE-AC=BE-BD，即CE=DE，
在△OAE与△ODE中，
∵
|
∴△OAE≌△ODE（SAS），
∴OC=OD．
点评：本题考查的是垂径定理，熟知垂直弦的直径平分弦是解答此题的关键．
练习册系列答案
相关题目
小明到商店为自己和弟弟各买一套相同的衣服，甲、乙两个商店的每套衣服售价相同，甲店的优惠数是：若一次买两套则其中一套可获得7折优惠；乙店的优惠数是：若一次买两套，则享受总价的8折优惠，你认为（ ）
| A、甲店比乙店优惠 |
| B、乙店比甲店优惠 |
| C、甲、乙两家都一样 |
| D、以上都有可能 |