题目内容
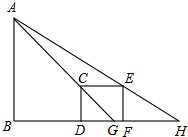如图，为测量山峰AB的高度，在D处和F处竖立标杆DC和FE，标杆的高都是4米，相隔50米，并且AB、CD和EF在同一平面内，从标杆DC退后2米到G处可以看到山峰和标杆顶点C在同一直线上，从标杆FE退后4米到H处可以看到山峰A和标杆顶端E在同一直线上，求山峰高度AB及其与标杆CD的水平距离BD的长．考点：相似三角形的应用
专题：
分析：根据题意可得出△CDG∽△ABG，△EFH∽△ABH，再根据相似三角形的对应边成比例即可得出结论．
解答：解：∵AB⊥BH，CD⊥BH，EF⊥BH，
∴AB∥CD∥EF，
∴△CDG∽△ABG，△EFH∽△ABH，
∴
=
，
=
，
∵CD=DG=EF=2m，DF=52m，FH=4m，
∴
=
，
=
，
∴
=
，
解得BD=52m，
∴
=
，
解得AB=54m．
∴AB∥CD∥EF，
∴△CDG∽△ABG，△EFH∽△ABH，
∴
| CD |
| AB |
| DG |
| DG+BD |
| EF |
| AB |
| FH |
| FH+DF+BD |
∵CD=DG=EF=2m，DF=52m，FH=4m，
∴
| 2 |
| AB |
| 2 |
| 2+BD |
| 2 |
| AB |
| 4 |
| 52+4+BD |
∴
| 2 |
| 2+BD |
| 4 |
| 4+52+BD |
解得BD=52m，
∴
| 2 |
| AB |
| 2 |
| 2+52 |
解得AB=54m．
点评：本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例是解答此题的关键．
练习册系列答案
相关题目