Question

1．在楼顶A处测得地面B，C两建筑物的俯角分别是30°，45°，且楼A与B，C两建筑物在同一条直线上．已知B，C两建筑物之间的距离为20m，则楼高为27.3米．（忽略B，C两建筑物的高度，结果精确到0.1m）

Answer 1

分析 设窗口A到地面的高度AD为xm，根据题意在直角三角形ABD和直角三角形ACD中，利用锐角三角函数用含x的代数式分别表示线段BD和线段CD的长，再根据BD-CD=BC=6列出方程，解方程即可．

解答 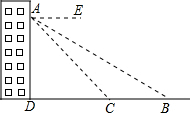解：设窗口A到地面的高度AD为xm．
由题意得：∠ABC=30°，∠ACD=45°，BC=20m．
∵在Rt△ABD中，BD=$\frac{AD}{tan30°}$=$\sqrt{3}$xm，
在Rt△ADC中，CD=$\frac{AD}{tan45°}$=xm，
∵BD-CD=BC=20，
∴$\sqrt{3}$x-x=20，
∴x=10$\sqrt{3}$+10≈27.3．
答：窗口A到地面的高度AD为27.3米．
故答案为：27.3米．

点评 本题考查了解直角三角形的应用，解题的关键是从实际问题中整理出直角三角形并选择合适的边角关系求解．