题目内容
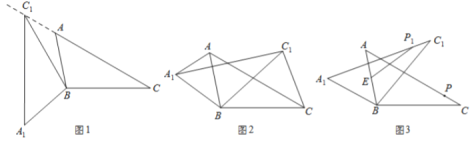
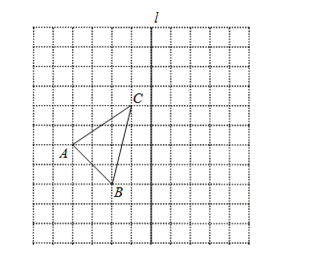
【题目】如图，在
的正方形网格中，每个小正方形的边长都为1，网格中有一个格点
（即三角形的顶点都在格点上）．
（1）在图中作出
关于直线l对称的
；（要求A与
，B与
，C与
相对应）
（2）作出绕点C顺时针方向旋转90°后得到的
；
（3）在（2）的条件下求出线段CB在旋转中所扫过的面积．（结果保留π）
【答案】（1）见解析（2）见解析（3）
π.
【解析】
（1）根据网格结构找出点A、B、C关于直线l的对称点
、
、
的位置，然后顺次连接即可；
（2）根据网格结构找出点A、B绕点C顺时针方向旋转90°后的A
、B的位置，然后与点C顺次连接即可；
（3）利用勾股定理列式求出BC，再根据扇形的面积公式列式计算即可得解．
(1) 
如图所示；
(2) 
如图所示；
(3)根据勾股定理,BC=
=
,
所以,线段CB旋转到CB2所扫过的面积S=
=π.
练习册系列答案
小学课时特训系列答案
相关题目
