题目内容
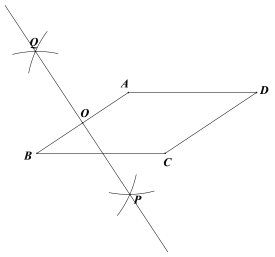
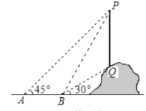
【题目】如图,从点![]() 看一山坡上的电线杆
看一山坡上的电线杆![]() ,观测点
,观测点![]() 的仰角是
的仰角是![]() ,向前走
,向前走![]() 到达
到达![]() 点, 测得顶端点
点, 测得顶端点![]() 和杆底端点
和杆底端点![]() 的仰角分别是
的仰角分别是![]() 和
和![]() ,则该电线杆
,则该电线杆![]() 的高度( )
的高度( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
延长PQ交直线AB于点E,设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则问题求解.
解:延长PQ交直线AB于点E,设PE=x.

在直角△APE中,∠A=45°,
则AE=PE=x;
∵∠PBE=60°
∴∠BPE=30°
在直角△BPE中,BE=![]() PE=
PE=![]() x,
x,
∵AB=AE-BE=6米,
则x-![]() x=6,
x=6,
解得:x=9+3![]() .
.
则BE=3![]() +3.
+3.
在直角△BEQ中,QE=![]() BE=
BE=![]() (3
(3![]() +3)=3+
+3)=3+![]() .
.
∴PQ=PE-QE=9+3![]() -(3+
-(3+![]() )=6+2
)=6+2![]() .
.
答:电线杆PQ的高度是(6+2![]() )米.
)米.
故选:A.

练习册系列答案
相关题目
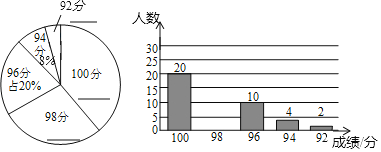
【题目】为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了一次调查,并将调査结果绘制成如下不完整的统计表和统计图.
学生选修课程统计表
课程 | 人数 | 所占百分比 |
声乐 | 14 |
|
舞蹈 | 8 |
|
书法 | 16 |
|
摄影 |
|
|
合计 |
|
|

根据以上信息,解答下列问题:
(1)![]() ,
,![]() .
.
(2)求出![]() 的值并补全条形统计图.
的值并补全条形统计图.
(3)该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.
(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.