题目内容
15.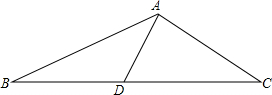 如图,在△ABC中,AC=4cm,BC=10cm,BC边上的中线AD=3cm,求△ABD的面积.
如图,在△ABC中,AC=4cm,BC=10cm,BC边上的中线AD=3cm,求△ABD的面积.
分析 由AD是BC边上的中线,得到△ABD的面积=△ADC的面积,根据勾股定理的逆定理推出∠DAC=90°,由三角形的面积公式直接求出结论.
解答 解:∵AD是BC边上的中线,
∴BD=DC=5,△ABD的面积=△ADC的面积,
∵AD2+AC2=32+42=52=DC2,
∴∠DAC=90°,
∴△ADC的面积=$\frac{1}{2}AD•AC=\frac{1}{2}×3×4=6$cm2,
∴△ABD的面积=6cm2.
点评 本题主要考查了三角形的中线,勾股定理逆定理,三角形面积的求法,掌握三角形中线把三角形分成两个面积相等的三角形是解决问题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
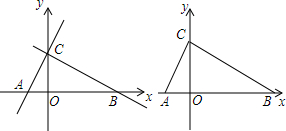
4. 如图,将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )
如图,将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )
 如图,将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )
如图,将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )| A. | 65° | B. | 75° | C. | 85° | D. | 不能确定 |
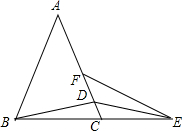 如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.
如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.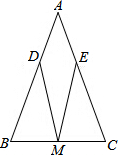 如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE,
如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE, 如图,直角坐标系中.点A的坐标为(1,0),以线段OA为边在第四象限内作等边点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中.点A的坐标为(1,0),以线段OA为边在第四象限内作等边点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
 如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.
如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.