题目内容
5. 如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.
如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.(1)说明MN=$\frac{1}{2}$AB;
(2)若把条件“点C在线段AB上”改为“点C在线段AB的延长线上”,结论又如何?请说明理由.
分析 (1)由线段中点的定义可知:MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,然后根据MN=MC+NC可得到MN=$\frac{1}{2}$AB;
(2)先根据题意画出图形,由中点的定义可知MC=$\frac{1}{2}AC$,NC=$\frac{1}{2}$CB,由MN=MC-NC可得到MN=$\frac{1}{2}AB$.
解答 解:(1)∵M是AC的中点,
∴MC=$\frac{1}{2}$AC.
∵N是BC的中点,
∴CN=$\frac{1}{2}$BC.
∵MN=MC+NC,
∴MN=$\frac{1}{2}AC+\frac{1}{2}BC$=$\frac{1}{2}(AC+BC)$=$\frac{1}{2}$AB.
(2)如图所示:
∵M是AC的中点,
∴MC=$\frac{1}{2}AC$.
∵N是BC的中点,
∴NC=$\frac{1}{2}$CB.
∴MN=MC-NC=$\frac{1}{2}AC-\frac{1}{2}CB$=$\frac{1}{2}(AB+CB)$-$\frac{1}{2}BC$=$\frac{1}{2}AB+\frac{1}{2}$BC-$\frac{1}{2}$BC=$\frac{1}{2}AB$.
点评 本题主要考查的是两点间的距离,掌握线段中点的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
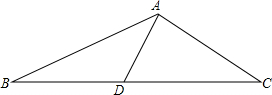 如图,在△ABC中,AC=4cm,BC=10cm,BC边上的中线AD=3cm,求△ABD的面积.
如图,在△ABC中,AC=4cm,BC=10cm,BC边上的中线AD=3cm,求△ABD的面积. 选取合适的比例,画出如图所示物体的三视图.单位:mm.
选取合适的比例,画出如图所示物体的三视图.单位:mm.
 已知∠AOB=80°,OE,OC分别平分∠AOD与∠BOD,∠COD=15°,求∠DOE的度数.
已知∠AOB=80°,OE,OC分别平分∠AOD与∠BOD,∠COD=15°,求∠DOE的度数.