题目内容
19.已知关于x的一元二次方程x2-6x-k2=0(k为常数).(1)求证:方程有两个不相等的实数根;
(2)设x1、x2为方程的两个实数根,且2x1+x2=14,试求出方程的两个实数根和k的值.
分析 (1)根据方程的各项系数结合根的判别式即可得出△=4k2+36≥36,由此即可得出结论;
(2)根据根与系数的关系可得出x1+x2=6①、x1•x2=-k2,结合2x1+x2=14②,联立①②成方程组,解方程组即可得出方程的两根,再将其代入x1•x2=-k2中,即可得出k的值.
解答 (1)证明:在方程x2-6x-k2=0中,△=(-6)2-4×1×(-k2)=4k2+36≥36,
∴方程有两个不相等的实数根.
(2)解:∵x1、x2为方程的两个实数根,
∴x1+x2=6①,x1•x2=-k2,
∵2x1+x2=14②,
联立①②成方程组$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=6}\\{2{x}_{1}+{x}_{2}=14}\end{array}\right.$,
解之得:$\left\{\begin{array}{l}{{x}_{1}=8}\\{{x}_{2}=-2}\end{array}\right.$,
∴x1•x2=-k2=-16,
∴k=±4.
点评 本题考查了根的判别式以及根与系数的关系,熟练掌握当△>0时方程有两个不相等的实数根是解题的关键.

练习册系列答案
相关题目
9.在-|-2|,|-(-2)|,-(+2),-(-$\frac{1}{2}$),+(-2),-π,0中,负有理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
10.计算:$\sqrt{2}$cos45°的结果等于( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
14. 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为12,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为12,则k的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为12,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为12,则k的值为( )| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
11.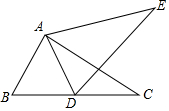 如图,将△ABC绕点A逆时针旋转40°得到△ADE,其中点D恰好落在BC边上,则∠ADE等于( )
如图,将△ABC绕点A逆时针旋转40°得到△ADE,其中点D恰好落在BC边上,则∠ADE等于( )
 如图,将△ABC绕点A逆时针旋转40°得到△ADE,其中点D恰好落在BC边上,则∠ADE等于( )
如图,将△ABC绕点A逆时针旋转40°得到△ADE,其中点D恰好落在BC边上,则∠ADE等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |