题目内容
9.若c、d互为相反数,x的绝对值是1,且ab=-$\frac{1}{2}$,求$\frac{c+d}{x}$-2ab+x2的值.分析 由题意可知:c+d=0,ab=-$\frac{1}{2}$,x=±1,然后代入求值即可.
解答 解:∵c、d互为相反数,且ab=-$\frac{1}{2}$,x的绝对值是1,
∴ab=$-\frac{1}{2}$,c+d=0,x=±1.
当x=1时,原式=0-2×$(-\frac{1}{2})$+1=2;
当x=-1时,原式=0-2×$(-\frac{1}{2})$+1=2.
综上所述:$\frac{c+d}{x}$-2ab+x2的值为2.
点评 本题主要考查的是求代数式的值,掌握相反数,绝对值的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列各数中,是无理数的是( )
| A. | $\sqrt{2}$ | B. | $\root{3}{8}$ | C. | $\sqrt{16}$ | D. | $\frac{1}{3}$ |
4.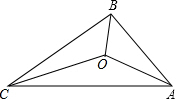 如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )
如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )
 如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )
如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )| A. | 1:1:1 | B. | 1:2:3 | C. | 2:3:4 | D. | 3:4:5 |
14.2016年,我国约有9400000人参加高考,将9400000用科学记数法表示为( )
| A. | 9.4×105 | B. | 9.4×106 | C. | 0.94×106 | D. | 94×104 |
18. 如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )
如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )
 如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )
如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )| A. | 0 | B. | 2 | C. | 4 | D. | 10 |