题目内容
15. 已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的作直线EF⊥BD分别交AD,BC于E,F两点,连结BE,DF.求证:四边形BFDE为菱形.
已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的作直线EF⊥BD分别交AD,BC于E,F两点,连结BE,DF.求证:四边形BFDE为菱形.
分析 根据平行四边形的性质以及全等三角形的判定方法证明出△DOE≌△BOF,得到OE=OF,利用对角线互相平分的四边形是平行四边形得出四边形EBFD是平行四边形,进而利用对角线互相垂直的平行四边形是菱形得出四边形BFDE为菱形.
解答 证明:∵在?ABCD中,O为对角线BD的中点,
∴BO=DO,∠EDB=∠FBO,
在△EOD和△FOB中,
$\left\{\begin{array}{l}{∠EDO=∠FBO}\\{OD=OB}\\{∠EOD=∠FOB}\end{array}\right.$,
∴△DOE≌△BOF(ASA);
∴OE=OF,
又∵OB=OD,
∴四边形EBFD是平行四边形,
∵EF⊥BD,
∴四边形BFDE为菱形.
点评 此题主要考查了菱形的判定,平行四边形的性质以及全等三角形的判定与性质等知识,得出OE=OF是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.盐城城市快速路网是我市建市史上单项投资规模最大的城市交通工程建设项目,计划2016年底建成通车,项目预算投资130亿元,130亿用科学记数法表示为( )
| A. | 130×108 | B. | 1.3×109 | C. | 1.3×1010 | D. | 1.3×1011 |
3. 如图,AB∥CD,AE交CD于C,∠A=35°,∠DEC=90°,则∠D的度数为( )
如图,AB∥CD,AE交CD于C,∠A=35°,∠DEC=90°,则∠D的度数为( )
 如图,AB∥CD,AE交CD于C,∠A=35°,∠DEC=90°,则∠D的度数为( )
如图,AB∥CD,AE交CD于C,∠A=35°,∠DEC=90°,则∠D的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
7. 如图,锐角三角形ABC中,直线l为BC的垂直平分线,射线m平分∠ABC,l与m相交于P点.若∠A=60°,∠ACP=24°,则∠ABP等于( )
如图,锐角三角形ABC中,直线l为BC的垂直平分线,射线m平分∠ABC,l与m相交于P点.若∠A=60°,∠ACP=24°,则∠ABP等于( )
 如图,锐角三角形ABC中,直线l为BC的垂直平分线,射线m平分∠ABC,l与m相交于P点.若∠A=60°,∠ACP=24°,则∠ABP等于( )
如图,锐角三角形ABC中,直线l为BC的垂直平分线,射线m平分∠ABC,l与m相交于P点.若∠A=60°,∠ACP=24°,则∠ABP等于( )| A. | 24° | B. | 30° | C. | 32° | D. | 42° |
4.记n边形(n>3)的一个外角的度数为p,与该外角不相邻的(n-1)个内角的度数的和为q,则p与q的关系是( )
| A. | p=q | B. | p=q-(n-1)•180° | C. | p=q-(n-2)•180° | D. | p=q-(n-3)•180° |
 如图是由几个正方体组成的立体图形,则这个立方体从左看到的平面图形是( )
如图是由几个正方体组成的立体图形,则这个立方体从左看到的平面图形是( )



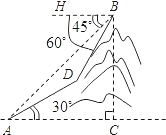 如图,我校九年级一个学习小组进行测量小山高度的实践活动,部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°,请你帮助他们计算出小山BC的高度(结果保留根号).
如图,我校九年级一个学习小组进行测量小山高度的实践活动,部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°,请你帮助他们计算出小山BC的高度(结果保留根号).