Question

13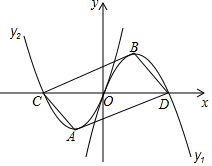．如图，过原点的两条抛物线y₁=mx²+nx，（m＜0，n＞0），y₂=-mx²+nx，（m＜0，n＞0），它们与x轴的另一个交点分别为D、C，顶点分别为B、A，若以点A、B、C、D为顶点的四边形为矩形时，n的值为2$\sqrt{3}$．

Answer 1

分析 首先证明△AOC，△BOD都是等边三角形，再根据BD=OD，列出方程即可解决问题．

解答 解：∵四边形ABCD是矩形，
∴OC=OD=OA=OB，
又根据对称性可知，AC=AO，BO=BD，
∴AC=AO=CO，OB=OD=BD，
∴△AOC，△BOD是等边三角形，
∵D（-$\frac{n}{m}$，0），B（-$\frac{n}{2m}$，-$\frac{{n}^{2}}{4m}$），
∴（-$\frac{n}{m}$）²=（（-$\frac{n}{m}$+$\frac{n}{2m}$）²+（$\frac{{n}^{2}}{4m}$）²，
∵m＜0，n＞0，
∴解得n=2$\sqrt{3}$．
故答案为2$\sqrt{3}$．

点评 本题考查抛物线与x轴的交点、矩形的性质、等边三角形的判定和性质、两点之间的距离公式等知识，解题的关键是学会利用参数构建方程解决问题，属于中考填空题中的压轴题．