题目内容
4.如图1,在平面直角坐标系xOy中,点A在第二象限,过点A作AB⊥x轴于B,AC⊥y轴于C,若点A在直线y=-x上,且OA=3$\sqrt{2}$.(1)求OB的长;
(2)如图2,设N(0,n)是y轴上一动点,连结AN,作AM⊥AN,交x轴于点M(m,0),
①求m关于n的函数关系式;
②设直线y=-x与直线MN相交于点T,求当OM=$\frac{1}{3}$OB时的T点坐标.

分析 (1)根据已知条件得到四边形ABOC是正方形,根据正方形的性质得到AB=OB,即可得到结论;
(2)根据全等三角形的性质得到BM=CN,于是得到m-(-3)=n-3,即可得到结论;②∵根据已知条件得到M(-1,0),N(0,5),求得直线MN的解析式为:y=5x+5,解方程组即可得到结论.
解答 解:(1)∵点A作AB⊥x轴于B,AC⊥y轴于C,
∴∠ABO=∠ACO=90°,
∵∠BOC=90°,
∴四边形ABOC是矩形,
∵点A在直线y=-x上,
∴OA平分∠BOC,
∴AB=AC,
∴矩形ABOC是正方形,
∴AB=OB,
∵OA=3$\sqrt{2}$,
∴OB=$\frac{\sqrt{2}}{2}$OA=3;
(2)①∵∠CAB=∠MAN=90°,
∴∠BAM=∠NAC,
在△ABM与△ACN中,$\left\{\begin{array}{l}{∠ABM=∠ACN=90°}\\{∠BAM=∠CAN}\\{AB=AC}\end{array}\right.$,
∴△ABM≌△ACN,
∴BM=CN,
即m-(-3)=n-3,
∴n=m+6;
②∵OM=$\frac{1}{3}$OB=$\frac{1}{3}$×3=1,
∴M(-1,0),N(0,5),
设直线MN的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{o=-k+b}\\{5=b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=5}\\{b=5}\\{\;}\end{array}\right.$
∴直线MN的解析式为:y=5x+5,
解$\left\{\begin{array}{l}{y=5x+5}\\{y=-x}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{5}{6}}\\{y=\frac{5}{6}}\end{array}\right.$,
∴T点坐标为(-$\frac{5}{6}$,$\frac{5}{6}$).
点评 本题考查了求一次函数的解析式,正方形的判定和性质,全等三角形的判定和性质,求直线的交点坐标,正确的理解题意是解题的关键,

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| A. | y=3x-2 | B. | y=-3x-2 | C. | y=3x+2 | D. | y=-3x+2 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 626 | B. | 288 | C. | 168 | D. | 624 |
 如图,在四边形ABCD中,AD∥BC,AD=12cm,CD=8cm,BC=BD=20cm,点P由B出发沿BD方向匀速运动,速度为2cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为2cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:
如图,在四边形ABCD中,AD∥BC,AD=12cm,CD=8cm,BC=BD=20cm,点P由B出发沿BD方向匀速运动,速度为2cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为2cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题: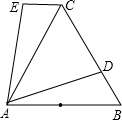 如图,△ABC为等边三角形,D是BC边上一点,AB=10,AD=9,△ABD经过旋转60°后到达△ACE的位置,
如图,△ABC为等边三角形,D是BC边上一点,AB=10,AD=9,△ABD经过旋转60°后到达△ACE的位置,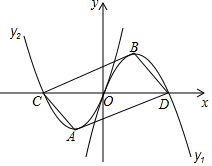 如图,过原点的两条抛物线y1=mx2+nx,(m<0,n>0),y2=-mx2+nx,(m<0,n>0),它们与x轴的另一个交点分别为D、C,顶点分别为B、A,若以点A、B、C、D为顶点的四边形为矩形时,n的值为2$\sqrt{3}$.
如图,过原点的两条抛物线y1=mx2+nx,(m<0,n>0),y2=-mx2+nx,(m<0,n>0),它们与x轴的另一个交点分别为D、C,顶点分别为B、A,若以点A、B、C、D为顶点的四边形为矩形时,n的值为2$\sqrt{3}$.